Асимптотический метод расчета пластин
Для прямоугольной пластины с закреплением, отличным от шарнирного опирания по противолежащим сторонам, применяют различные приближенные методы. Рассмотрим асимптотический метод.
В пластинках так же как и в балках, имеет место динамический краевой эффект, который заключается в том, что закрепление влияет на форму колебания только вблизи границы, а вдали от нее форма колебания определяется произведением синусов типа уравнения (321). Благодаря этому колебания можно представить как сумму функции типа (321) и быстро затухающих с удалением от границ функций, которые позволяют выполнить граничные условия.
Рассмотрим применение этого метода на примере заделанной по контуру прямоугольной пластины размерами




Вблизи границ


где

Аналогично вблизи границ


Таким образом, общее выражение для


В средней части пластинки функции



Вблизи границ


Выполняя дифференцирование, приходим к уравнению:

которое распадается на два уравнения:

Так как



где

В силу симметрии вблизи стороны


Аналогично вблизи стороны


где

и вблизи стороны


Рассмотрим граничные условия при


При вычислении






Для одновременного выполнения этих уравнений необходимо, чтобы определитель, составленный из коэффициентов при



Аналогично условия при


Так как






Рассмотрим, например, колебания квадратной пластинки с одинаковым числом узловых линий в направлениях




откуда

Частоты колебаний определяются формулой:

Достаточно хороший результат получается уже для низшей частоты:

Точное значение:

Как видно из вышеизложенного, при использовании асимптотического метода погрешность возникает вследствие приближенного выполнения граничных условий вблизи угловых точек.
Бегущие волны в круглых пластинках
Рассмотренные выше собственные колебания круглых пластинок описываются уравнением

Они соответствуют стоячим волнам на поверхности пластинки, при которых узловые диаметры неподвижны.
Наряду с (330) решением уравнения движения является также выражение

Но поскольку уравнение движения линейно, сумма и разность (330) и (331) также являются его решениями:


Эти выражения представляют собой уравнения бегущих волн. Первое выражение соответствует вращению всей картины деформаций вокруг оси симметрии пластинки в направлении возрастания угла


Если имеются внешние нагрузки, вращающиеся по периферии пластинки со скоростью, близкой к скорости

Практически движущаяся по круглой пластинке нагрузка осуществляется в дисках турбомашин благодаря вращению диска при неподвижной в пространстве нагрузке, обусловленной неравномерностью давления рабочего тела по окружности.
Критические скорости вращения диска



где


Частотное уравнение и собственные формы
Развёрнутая запись граничных условий приводит к однородным уравнениям относительно постоянных C1, C2, C3, C4.
Чтобы эти постоянные не равнялись нулю, должен равняться нулю определитель, составленный из коэффициентов системы; это приводит к частотному уравнению. При этих операциях выясняются соотношения между C1, C2, C3, C4, т.е. определяются собственные формы колебаний (с точностью до постоянного множителя).
Проследим составление частотных уравнений на примерах.
Для балки с шарнирно-опёртыми концами согласно (203) имеем следующие граничные условия: X=0; X''=0 при x=0 и x=


Чтобы C2 и C4 не были равны нулю, необходимо равенство нулю определителя:

Таким образом, частотное уравнение имеет вид

Подставляя выражения T и U, получим

Так как


Корни этого уравнения:

Учитывая (196), получим

Перейдём к определению собственных форм. Из записанных выше однородных уравнений вытекает следующее соотношение между постоянными C2 и C4:

Следовательно, (197) приобретает вид

или

Согласно (207), имеем

где

Действие двух гармонических сил с близкими частотами биения
Если система с одной степенью свободы испытывает действие двух различных гармонических возмущающих сил, то вследствие её линейности суммарный эффект может быть определён путём сложения эффектов, вызываемых каждой из сил. Так, возмущающая сила вида

вызовет сложные колебания

Если частоты



=

или

где


Обозначая


Вследствие того, что частоты







где



Итак, движение будет носить почти синусоидальный характер, причём амплитуда колебаний А есть медленно изменяющаяся функция времени. Период изменения амплитуды А (период биений) составляет
TA=

Так как разность


Биения могут возникнуть и при действии одной возмущающей силы



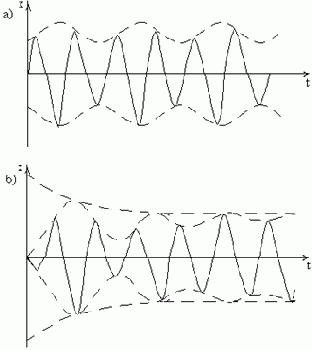
Рис. 43
Действие гармонической силы
Случай, когда возмущающая сила изменяется по гармоническому закону
F=F0 sin pt, (94)
где F0 - амплитуда силы; p - её частота, является наиболее распространённым в практике.
Описание колебательного процесса, вызываемого такой силой, при нулевых начальных условиях можно получить при помощи (89)

Вычисляя интеграл, при


Заменим



Из (97) следует, что при нулевых начальных условиях возникают сложные колебания, состоящие из двух частей: колебаний, происходящих с частотой p возмущающей силы, и колебаний, происходящих с собственной частотой

Составляющая, названная выше свободными колебаниями, быстро исчезает, поэтому достаточно ограничиться изучением стационарной, незатухающей части решения

Амплитуда вынужденных колебаний

отличается от прогиба



Динамический коэффициент




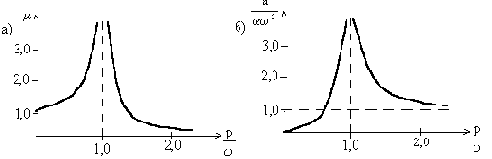
Рис. 41
При малой частоте возмущающей силы динамический коэффициент близок к единице. С ростом частоты p динамический коэффициент быстро увеличивается и при

Это соответствует состоянию резонанса, когда амплитуда вынужденных колебаний стремится к бесконечности (если учесть силы неупругого сопротивления, то амплитуда при резонансе окажется хотя и ограниченной, но обычно настолько значительной, что состояние резонанса всё равно следует считать опасным).
Если частота p больше собственной частоты



В приведенных рассуждениях считалось, что амплитудное значение возмущающей силы не связано с её частотой. Однако чаще бывает обратное, например, при вращении неуравновешенного ротора на опоры передаётся возмущающая сила

где


В данном случае амплитуда возмущающей силы





Амплитуда стационарных колебаний при этом определяется выражением


в котором параметр системы

На рис.41,б представлено изменение амплитуды колебаний в зависимости от отношения

Как видно, при



Остановимся подробнее на случае совпадения частот


Рис. 42
При этом интеграл (95) принимает вид

После вычисления получим

График этого движения показан на рис.42. Как видно, при совпадении частот амплитуда нарастает по линейному закону и за конечный промежуток времени не обращается в бесконечность. Из этого вытекает принципиальная возможность перехода через резонанс, так как в процессе разгона двигателей равенство

Действие непериодической возмущающей силы
1. Действие линейно возрастающей силы (рис.38,а)
Используем выражение (91), полагая


График этого движения показан на рис.38,б.

Перемещения нарастают по сложному закону, представляющему собой сумму синусоиды и линейной функции. Дополнительное синусоидальное колебание тем существеннее, чем быстрее нарастает сила F, т.е. чем больше а.
Колебания подрессоренного груза при движении по неровной дороге (рис.39)
Пусть профиль дороги задан уравнением


где h - предел, к которому стремится высота профиля;

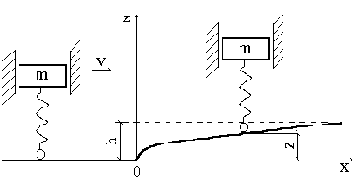
Рис. 39
Обозначим через V скорость движения груза массой m и примем начало отсчёта времени в мгновение, когда опорная точка проходит начало неровности. Тогда х=Vt и движение опорной точки по вертикали определяется законом

Дифференцируя, находим

На основании (92) получим закон движения груза по вертикали:
Z=f(t)-

Так как важным является не абсолютное изменение положения груза, а его колебания относительно опорной точки, то рассмотрим разность, определяющую дополнительную деформацию пружины




Интегрируя, находим


где


Отсюда следует, что при весьма малой скорости параметр





2. Действие медленно изменяющихся сил
Рассмотрим полученное выше решение задачи о вынужденных колебаниях (91). Первое слагаемое представляет собой статическое отклонение, вызванное силой F(t). Второе слагаемое - это поправка к статическому отклонению, причём эта поправка зависит от скорости изменения силы

При малой скорости нарастания внешней нагрузки динамическая поправка к статическому решению относительно мала и нагружение практически можно рассматривать как статическое.
А.Н.Крылов дал оценку динамической поправки для общего случая возмущающей силы. Если кривая F(t) имеет один максимум (рис.40,а), то, обозначая максимальное значение



Произведение



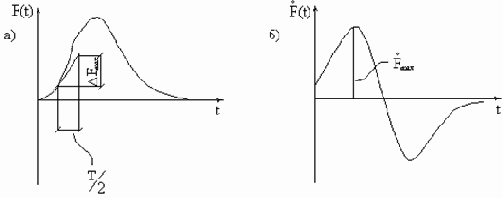
Рис. 40
Если сила возрастает равномерно в течение времени t0, то


Её относительная величина

Отсюда следует, что если период свободных колебаний мал по сравнению с продолжительностью действия силы, то она может считаться медленно изменяющейся, а её действие можно рассчитывать без учёта динамичности, т.е. считать силу приложенной статически.
3. Действие быстро исчезающих сил
Пусть возмущающая нагрузка действует в течение весьма короткого промежутка времени. Даже значительная нагрузка может оказаться безопасной, если длительность её действия мала по сравнению с периодом свободных колебаний системы.
Рассмотрим действие силы F, которая внезапно прикладывается в момент времени t=0, действует в течение некоторого промежутка времени а, а затем также внезапно исчезает. Можно показать, что если a<


Обозначим отношение промежутка времени а к периоду свободных колебаний Т через


Максимальное отклонение в соответствии с (93):

Следовательно, динамический коэффициент:


Значения динамического коэффициента


Таблица 5
 |
0 |
0,01 |
0,02 |
0,03 |
0,05 |
0,10 |
0,15 |
0,25 |
0,5 |
 |
0 |
0,062 |
0,126 |
0,188 |
0,313 |
0,618 |
0,908 |
1,413 |
2,000 |
Покажем, что действие кратковременной силы приближённо можно оценить её импульсом. Для t>à решение имеет вид

или

=

Но так как отношение



Тогда приближённо можно записать

Входящий сюда интеграл есть импульс силы F(t), т.е. движение системы определяется величиной импульса кратковременной силы, причём подробности изменения силы за промежуток времени а не играют роли.
Действие периодических импульсов
Исследуем действие периодических импульсов (рис.44,б), считая длительность каждого из них исчезающе малой.
Рассмотрим какой-либо период Т, принимая начало отсчёта времени в конце действия предшествующего импульса (например, в момент времени




В течение рассматриваемого периода (до приложения следующего импульса) колебания являются свободными и происходят с собственной частотой


и, следовательно,

В конце этого периода, непосредственно перед следующим импульсом (мгновение



В результате действия очередного импульса скорость мгновенно изменится на величину




Вследствие периодичности процесса эти величины должны быть равны




Решая уравнения, находим




Закон движения (104) принимает вид

Замкнутая форма этого решения позволяет легко исследовать влияние периодических ударов, в то время как способ разложения на гармонические составляющие привёл бы к бесконечным суммам.
Амплитуда колебаний определяется формулой:

Дробь


можно назвать коэффициентом повторности. Этот коэффициент характеризует возрастание влияния повторных импульсов. Из формулы для величины




Действие произвольной периодической
В практических приложениях часто встречаются периодические возмущающие силы более сложного характера, чем рассмотренные выше.
Так, на рис.44,а показан закон изменения крутящего момента, создаваемого четырёхтактным двигателем внутреннего сгорания. Другой пример – периодические "безмассовые" удары – показан на рис.44,б.
Силы (моменты) рассматриваемого вида имеют чётко выраженный период колебаний Т, но не описываются единым аналитическим выражением. В подобных случаях чаще всего пользуются разложением периодической нагрузки в ряд Фурье. При этом сила представляется в виде суммы гармонических составляющих, а затем определяется эффект, вызываемый каждой из составляющих; после этого полученные частные эффекты суммируются.
Периодическую силу F(t) можно представить в виде ряда Фурье:

где

Коэффициенты







. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Рис. 44
Опираясь на решение (98), полученное для одной гармоники, находим

Это решение состоит из постоянного слагаемого



Рассмотренный способ чётко выявляет условия наступления резонанса. Недостатком этого способа является сложность вычислений, необходимых для учёта большого числа слагаемых в (103). Так, возмущающую силу, показанную на рис.44,a, для достаточной точности необходимо заменить примерно десятью гармониками.
Флаттер крыла в воздушном потоке
Как уже говорилось выше, флаттером называются автоколебания тел в потоке газа или жидкости.
При появлении первых скоростных самолетов флаттер служил причиной многочисленных катастроф. Явление флаттера тесно связано с теми воздействиями, которые поток воздуха оказывает на колеблющееся крыло.
Ограничимся рассмотрением принципиальной картины этого явления. При флаттере крыло самолета совершает изгибно-крутильные колебания, поэтому для анализа этого явления необходимо учесть по крайней мере две степени свободы крыла. При практических расчетах достаточно учесть движения крыла по первым формам собственных изгибных и крутильных колебаний. В еще более простом варианте расчета рассмотрим жесткое крыло, имеющее две степени свободы, соответствующие его вертикальному перемещению и повороту (рис.65).
Существенное значение имеет положение центра тяжести крыла, т.е. той точки его хорды, приложение вертикальной силы в которой вызывает только вертикальное перемещение крыла, но не его поворот. К этой точке (точка 0 на рис.65) будем приводить действующие на крыло силы.

Рис. 65
Если обозначить вертикальное перемещение центра жесткости крыла через






Сила инерции и момент сил инерции относительно точки 0 составляют соответственно

где



Наибольшие трудности представляет определение изменений аэродинамических сил, возникающих вследствие движения крыла. Простейшая гипотеза относительно этих сил состоит в том, что их можно вычислить так же, как и при неподвижном крыле, подставив в соответствующие формулы значения мгновенного угла атаки. В этом предположении получаем увеличение подъемной силы и момента

где




Формулы (166) представляют собой грубое приближение, так как в них полностью игнорируется влияние движения крыла на обтекание. Более точное решение задачи показывает, что если крыло совершает, например, гармонические колебания с частотой

Как величина присоединенной массы, так и фазовый сдвиг зависят от безразмерного параметра

Ради упрощения расчета не будем учитывать всех этих обстоятельств и дополнительно в первой из формул (166) пренебрежем слагаемым


где

Решение системы (167) отыщем в виде, соответствующем гармоническим колебаниям:

Подставляя (168) в (167), получим систему однородных алгебраических уравнений относительно



Приравнивая нулю определитель системы (169), получим частотное уравнение. Для того чтобы привести это уравнение к более простому виду, введем следующие обозначения:

- собственные частоты поступательных (изгибных) и крутильных колебаний крыла;

- относительная плотность крыла.
Тогда частотное уравнение можно представить в так:

При нулевой скорости потока V=0 это уравнение даёт два положительных значения W2, соответствующих двум собственным частотам системы.
С увеличением скорости потока возможно появление двух типов неустойчивости. Так, один из корней уравнения (170) может обратиться в нуль, что соответствует обращению в нуль свободного члена уравнения (170):

Обращение в нуль частоты собственных колебаний системы свидетельствует о её статической неустойчивости. Действительно, возвращаясь в формуле (171) к первоначальным обозначениям, приведём её к виду

Если это соотношение выполняется, то при повороте крыла на угол а момент дополнительной подъёмной силы

уравновешивается упругим моментом

Явление статической потери устойчивости крыла при достижении скоростью потока значения Vg называется дивергенцией.
Для крыльев самолётов, как правило, скорость дивергенции существенно превышает скорость полета и дивергенция не представляет реальной опасности.
Другой вид потери устойчивости – изгибно-крутильный флаттер - связан с тем, что частоты, определяемые из (170), становятся комплексными числами. Если имеются сопряжённые комплексные частоты


Экспоненциальные множители с действительными положительными показателями неограниченно возрастают.
Таким образом, в этом случае движение представляет собой колебания с нарастающими амплитудами (колебательный характер движения определяется множителями

Итак, условием наступления флаттера является появление комплексных корней уравнения (170), что происходит при обращении в нуль (назовём это «граничным условием») его дискриминанта:

Из уравнения (172) легко вычислить скорость флаттера.
Проследим на числовом примере характер изменения частоты свободных колебаний крыла по уравнению (170) при увеличении скорости потока.
Допустим, что





Этим данным соответствуют скорость дивергенции, вычисленная по уравнению (171),


График изменения частот колебаний системы в зависимости от скорости потока, построенный в соответствии с уравнением (170),показан на рис.66.
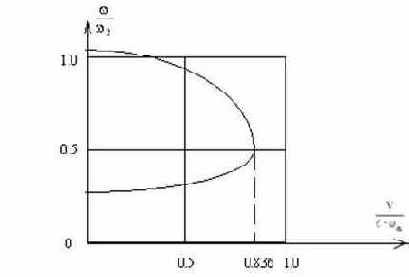
Рис. 66
При V=0 система имеет две частоты собственных колебаний, мало отличающиеся от частот чисто крутильных и чисто изгибных колебаний. С увеличением скорости потока частоты сближаются, и при скорости флаттера оказываются равными друг другу.
Наличие кратных собственных частот для консервативной системы не связано с какими-либо особенностями её поведения.Для неконсервативной системы, которую представляет собой крыло, находящееся в потоке воздуха, слияние двух частот ведёт к потере устойчивости движения. В процессе колебаний система начинает интенсивно потреблять энергию потока и амплитуды колебаний неограниченно возрастают. Механизм этого явления легко понять, если представить себе, что происходящие с одинаковой частотой крутильные и изгибные колебания крыла сдвинуты по фазе на

Формула Донкерлея
Так как метод Рэлея приводит к завышенному значению частоты колебаний, то весьма полезным является применение метода (формулы), дающего заниженное значение низшей частоты колебаний. Простейшей из такого рода формул является формула Донкерлея.
Рассмотрим какую-либо многомассовую систему, например балку (рис.74,а). Пусть на этом рисунке изображена точная форма собственных колебаний системы.

Рис. 74
Тогда точное значение собственной частоты системы выражается формулой

Теперь рассмотрим ту же балку, но только с одной массой mi
(рис.74, б). В этом случае частота колебаний будет определяться по формуле

где dii - податливость балки при приложении силы в точке расположения массы mi .
С другой стороны, приближённое значение wi той же частоты можно определить по формуле Рэлея, считая, что форма колебаний совпадает с изображённой на рис.74,а

Здесь По и xi имеют те же значения, что и в (275).
Так как форма, изображённая на рис.74,a, не является точной формой колебаний одномассовой системы, то выполняется неравенство:

Сравнивая (275) и (276), находим

Eсли в правой части полученного равенства заменить



Таким образом, приближенная формула Донкерлея всегда дает преуменьшенное значение частоты:

Рассчитав частоту одной и той же системы по методу Рэлея и формуле Донкерлея, получим вилку, в которой заключено истинное значение частоты колебаний.
Фрикционные автоколебания
Особого внимания заслуживают механические автоколебания, возникающие в системах с трением. Сила трения, которая в ранее рассмотренных примерах оказывалась причиной затухания колебаний, может явиться причиной их раскачивания.
Рассмотрим простейшую систему (рис.62,а), состоящую из двух вращающихся барабанов и бесконечной ленты.

Рис. 62
На ленте лежит груз массой


Для дальнейших рассуждений необходимо учесть, что сила трения R зависит от относительной скорости движения V (при заданном нормальном давлении груза, которое будем считать постоянным). Пусть характеристика трения имеет вид, показанный на рис.62,б, где значения V0 и R0 соответствуют состоянию равновесия груза.
Положим, что вследствие какого-либо возмущения в мгновение t=0 груз выведен из состояния покоя. Выясним характер движения, которое возникает после такого возмущения, считая, что скорость движения ленты в процессе колебаний груза не изменяется. Пусть в текущее мгновение




В это мгновение на груз действуют три силы: сила трения R, реакция пружины


Сила





где


Уравнение движения груза:

Подставляя сюда (162), получим

или

Сместим начало отсчета перемещений в точку


Тогда (163) имеет вид

Согласно (161), сумма двух последних слагаемых равна нулю, поэтому получим уравнение

Анализ структуры этого уравнения показывает, что с увеличением времени колебания должны исчезать, если сумма


Однако при небольших значениях







Природу «отрицательного затухания» при падающей характеристике трения можно выяснить исходя из следующих рассуждений. Когда груз движется вправо, т.е. по ходу движения ленты, относительная скорость скольжения уменьшается; вместе с этим сила трения увеличивается и ее приращение направлено вправо, т.е. также в сторону движения. В другом интервале движения, когда груз движется влево, приращение силы трения направлено также влево, т.е. опять в сторону движения. Такой характер изменения силы трения и является причиной возрастания колебаний.
Итак, для возрастания колебаний необходимо выполнение условия:


При помощи тех же рассуждений можно прийти к выводу о возможности автоколебаний упруго закрепленной колодки, прижатой к вращающемуся диску (рис.63,а), а также груза на пружине, когда левому ее концу задано движение с постоянной скоростью (рис.63,б). В обоих этих случаях необходимым условием автоколебаний также является наличие нисходящего участка характеристики трения.
К этому же классу явлений относятся автоколебания, возникающие при резании металлов на станках. Рассмотрим природу этих автоколебаний.
Со стороны заготовки на резец действует реакция






На резец действуют три силы: сила упругости - су системы резец-суппорт (где с - коэффициент жесткости); реакция заготовки



Рис. 63
Таким образом, уравнение движения системы резец-суппорт имеет вид

где

После линеаризации силы


Как установлено, неустойчивость состояния равновесия может быть обнаружена в предположении малости колебаний, т.е. при помощи линейного приближения. Однако, если отказаться от этого предположения и проследить за дальнейшим течением процесса, то обнаруживается, что рост амплитуд постепенно замедляется и в конечном итоге амплитуда полностью стабилизируется. Этот процесс установившихся (стационарных) автоколебаний (рис.64) называется предельным циклом.
Важной особенностью предельного цикла является его полная независимость от начальных условий; после любого возмущения состояния равновесия система приближается к одному и тому же предельному циклу.
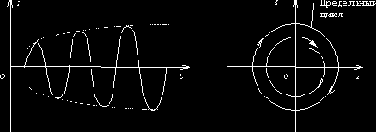
Рис. 64
Для выявления параметров (частоты, амплитуды) установившихся автоколебаний необходим анализ соответствующей нелинейной задачи.
В некоторых случаях стационарные автоколебания носят почти гармонический характер и совершаются с частотой свободных колебаний системы; соответствующие системы называются квазилинейными. В других случаях стационарные автоколебания резко отличаются от гармонических, сопровождаются остановками и скачками скорости; такие автоколебания и соответствующие системы называются релаксационными или разрывными.
Граничные условия
Для каждого конца стержня можно указать два граничных условия.
Свободный конец стержня (рис. 70,а). Нулю равны поперечная сила Q=EJX'''T и изгибающий момент M=EJX''T. Поэтому граничные условия имеют вид
X''=0; X'''=0 . (202)

Рис. 70
Шарнирно-опёртый конец стержня (рис.70,б). Нулю равны прогиб y=XT и изгибающий момент M=EJX''T. Следовательно, граничные условия таковы:
X=0 ; X''=0 . (203)
Защемленный конец (рис.70,в). Нулю равны прогиб y=XT и угол поворота

X=0; X'=0 . (204)
На конце стержня имеется точечный груз массы




В первом условии знак плюс принимается в случае, когда точечный груз связан с левым концом стержня, и знак минус, когда он связан с правым концом стержня. Второе условие вытекает из отсутствия изгибающего момента .
Упруго-опертый конец стержня (рис.70,д). Здесь изгибающий момент равен нулю, а поперечная сила Q=EJX'''T равна реакции опоры

Граничные условия:
X''=0 ;

(знак минус принимается в случае, когда упругая опора является левой, и знак плюс, когда она является правой).
Изгибные колебания балок
Рассмотрим случай, когда возмущающая нагрузка задана в виде сосредоточенной силы

или комбинации нескольких нагрузок того же вида с одинаковой частотой. Решение для прогибов будем искать в виде

сводя задачу к определению формы колебаний (кривой амплитуд прогибов)

В случае


Решение дифференциального уравнения (307) имеет вид

где


Для определения постоянных

1.Возмущающая сила


и граничное условие принимает вид

где знак «+» соответствует силе, приложенной к правому концу, знак «-» - силе, приложенной к левому концу. Кроме того,

2. Возмущающая сила

В этом сечении должны выполняться четыре условия сопряжения:

где а - абсцисса сечения, в котором приложена возмущающая сила; индексы «-» и «+» соответствуют сечениям, расположенным бесконечно близко слева и справа от сечения а.
Первые три условия обозначают непрерывность прогиба, угла поворота сечения и изгибающего момента в точке приложения возмущающей силы; четвертое условие выражает разрыв функции поперечной силы в указанном сечении на величину

Приведенные выше рассуждения представляют собой непосредственное решение задачи. Теперь рассмотрим другой способ - разложение решения в ряд по собственным функциям.
В общем случае, когда возмущающая поперечная нагрузка задана произвольным законом

дифференциальное уравнение движения приобретает вид

т.е. отличается от аналогичного уравнения при свободных колебаниях наличием правой части.
Как и выше, представим


Также в виде ряда будем искать решение для прогиба

Для определения функций времени




Эта формула совпадает по записи с (301), выведенной выше для продольных колебаний, но в (312)

Учитывая, что каждое слагаемое ряда (310) вызывает движение, описываемое соответствующим слагаемым ряда (311), можно записать уравнение (309) в виде

Разделив обе части на


Левая часть этого равенства равна


Отсюда получим дифференциальное уравнение для


Общее решение этого уравнения имеет вид

Изложенный способ позволяет получить решения и в случаях переменного сечения, если заранее найдены собственные формы


Кинематическое возбуждение колебаний
К такому же стандартному уравнению можно привести задачу о вынужденных колебаниях, вызываемых кинематическим способом. Рассмотрим вновь одномассовую систему, но предположим, что причиной колебаний груза m являются колебания точки крепления пружины (рис. 37). Пусть закон движения этой точки задан в виде f = f(t). Удлинение пружины в текущий момент времени равно x - f, а на груз действует сила упругости пружины - С(x - f), и дифференциальное уравнение движения

или

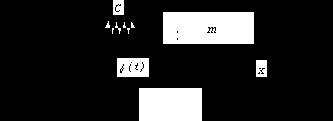
Рис. 37
Произведение Сf(t) можно считать приведенной возмущающей силой F(t), и тогда уравнение движения принимает стандартный вид (81).
Колебания оболочек
Изгибные колебания пластинок можно рассматривать независимо от их колебаний в своей плоскости. В отличие от этого при колебаниях оболочек изгиб стенки связан, как правило, с растяжением срединной поверхности. Потенциальная энергия деформации оболочки выражается формулой

где


Величина








Амплитудное значение кинетической энергии движения оболочки, совершающей гармонические колебания с частотой


Частота колебаний определяется формулой Рэлея

Числитель и знаменатель дроби (342) зависят от выбора функции перемещений




где


Величины






Если геометрия оболочки и условия ее закрепления это допускают, то наименьшие значения частот отвечают такому выбору функций


Но требование


Колебания, перпендикулярные плоскости кольца
В этом случае положение поперечного сечения кольца в процессе движения характеризуется смещением


Рис. 72
Установим зависимость моментов от перемещений. Так как задача линейная, то рассмотрим сначала силовые факторы, связанные со смещением х3, а затем - с х4.
Если х3 постоянно по длине окружности, то кольцо смещается как жёсткое целое, и внутренние силы не возникнут. Если х3 изменяется в зависимости от центрального угла по линейному закону


где GJкр- крутильная жёсткость бруса.
Если при этом отлична от нуля и вторая производная

меняется кривизна бруса и возникает изгибающий момент

где J1 - момент инерции сечения относительно центральной оси, лежащей в плоскости кривизны.
Найдём силовые факторы, связанные с поворотом х4. Если х4 постоянно, то происходит осесимметричный изгиб кольца, причём в его сечениях возникает изгибающий момент

При переменном по длине повороте х4 соседние сечения поворачиваются друг относительно друга и возникает крутящий момент

Суммируя силовые факторы, связанные с перемещениями х3 и х4, ,получаем

Составим уравнение движения элемента Rd

Будем пренебрегать инерцией поворота элемента вокруг своей оси.

Рис. 73
Условие динамического равновесия в направлении нормали к плоскости кольца приводит к уравнению:

Сумма моментов относительно нормали к оси элемента:

Сумма моментов относительно касательной к оси элемента:

Исключая поперечную силу из (257) и (258) и заменяя моменты в полученном уравнении и уравнении (259) их значениями (256), приходим к системе уравнений, в которую входят только перемещения х3 и х4:

Ограничиваясь исследованием собственных колебаний замкнутого
кольца, решение уравнений (260) можно представить в виде
x3 =Acoskj×coswt , x4 = Bcoskj×coswt . (261)
Подставляя значения (261) в уравнение движения (260), получим

Из равенства нулю определителя этой системы получим частотное уравнение, корни которого - собственные частоты - таковы:

Наименьшая отличная от нуля частота соответствует k=2.
Колебания пластин и оболочек
Задачи об определении частот и форм собственных колебаний пластин и оболочек приводят к необходимости интегрирования дифференциальных уравнений в частных производных. Наиболее хорошо изучены те случаи, когда оказывается возможным разделение переменных. К ним относятся, в частности, колебания прямоугольной пластины, шарнирно опертой по противолежащим сторонам, зонтичные и веерные колебания круглых осесимметричных пластин, колебания цилиндрических оболочек, замкнутых или шарнирно закрепленных вдоль образующих.
Если разделение переменных оказывается невозможным, то для расчета, в основном, используют приближенные и численные методы.
Колебания стержней переменного сечения
В тех случаях, когда распределённая масса и сечение стержня переменны по его длине, следует вместо уравнения продольных колебаний (175) исходить из уравнения

Уравнение крутильных колебаний (187) должно быть заменено уравнением

а уравнение поперечных колебаний (192) - уравнением

Уравнения (238)-(240) при помощи однотипных подстановок







и одному однотипному уравнению для функции

Уравнения (241)-(243) в отличие от уравнений, решённых выше, имеют переменные коэффициенты.
Замкнутую форму решений можно получить лишь в отдельных случаях, когда переменные

Колебания в плоскости кольца
Рассмотрим круговой брус малой кривизны постоянного сечения с радиусом R осевой линии (рис.71,а). Будем считать груз нерастяжимым. Перемещение центра тяжести поперечного сечения, зафиксированного угловой координатой






а б
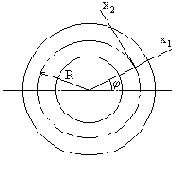

Рис. 71
Угол поворота поперечного сечения бруса в процессе движения определяется формулой

Изменение кривизны бруса



Изгибающий момент в поперечном сечении кольца:

Теперь составим уравнение движения элемента

Помимо перечисленных сил, на элемент действует также сила инерции:

где

Проектируя приложенные к элементу силы на радиус, получим

Равенство нулю суммы проекций всех сил на направление касательной приводит к уравнению:

Уравнение моментов имеет вид

Исключим из (248) и (249) нормальную силу N, а поперечную силу Q заменим её значением из (250):

Подставляя сюда значение M из (247), получим уравнение движения в перемещениях



Решение уравнения движения (252) будем искать в виде


При этом для



Согласно общим правилам решения дифференциальных уравнений, следует найти общее решение уравнения (253), включающее шесть постоянных, и подчинить его граничным условиям.
На каждом конце бруса должны быть равны нулю либо компоненты перемещений

Для замкнутого кольца граничные условия заменяются условиями периодичности, которые выполняются, если принять


Подставляя (254) в (253), устанавливаем, что последнее удовлетворяется тождественно, если

Формула (255) определяет частоты собственных колебаний кольца в своей плоскости. Значению


Кратные и нулевые корни частного уравнения
В некоторых случаях могут встречаться кратные корни частного уравнения, а в других случаях среди корней этого уравнения могут оказаться и нулевые.
Рассмотрим эти случаи на примере системы с двумя степенями свободы.
Из соответствующего такой системе частотного уравнения (39) следует, что при выполнении равенства

два корня частотного уравнения будут равны друг другу, а при выполнении равенства

один из корней частотного уравнения обращается в нуль.
В качестве примера рассмотрим свободные колебания плоской системы с двумя степенями свободы (рис.23).

Рис. 23
Обозначим через





После вычисления соответствующих производных уравнения
Лагранжа записываются так:

Предположим, что параметры рассматриваемой системы удовлетворяют двум простым (и практически реально осуществимым) соотношениям:


тогда полученные дифференциальные уравнения принимают более простую форму

Следовательно, инерционные коэффициенты и обобщённые коэффициенты жёсткости в этих уравнениях


и условие (49) выполняется, значит, рассматриваемая система имеет две одинаковые собственные частоты колебаний. Для выяснения этого можно было и не привлекать условие (49), так как из уравнений (51) непосредственно следует

Вследствие независимости уравнений (51) постоянные интегрирования одного уравнения не связаны с постоянными интегрирования другого уравнения

Для определения постоянных

Рассмотрим пример системы с одной нулевой собственной частотой (рис.24).

Рис. 24
Обозначим жёсткость вала на кручение через С; моменты инерции дисков относительно продольной оси системы - через


Крутильные колебания валов
Рассмотрим крутильные колебания многомассовой системы (рис. 26), которая является общепринятой эквивалентной схемой для расчёта крутильных колебаний коленчатых валов. Коленчатый вал приводится к эквивалентной схеме путём следующих замен: момент инерции заменяющего диска относительно оси вала должен быть равен моменту инерции колена относительно той же оси, при этом учитывается присоединённая масса шатуна; жёсткость на кручение участка заменяющего вала должна быть равна жёсткости на кручение соответствующего участка коленчатого вала.

Рис. 26
Эти замены являются неплохой аппроксимацией, хотя и не обеспечивают полной эквивалентности обеих схем. Приведенный момент инерции масс колена и шатуна изменяется в процессе вращения коленчатого вала, поэтому замена колена диском с постоянным моментом инерции не является строгой. Кроме того, при действии на коленчатый вал двух противоположно направленных пар деформация будет заключаться не только в закручивании участка между парами: вследствие изгиба произойдёт закручивание и других участков.
Тем не менее экспериментальные исследования подтверждают приемлемость эквивалентной схемы при достаточно тщательном определении эквивалентных моментов инерции и особенно эквивалентных жёсткостей.
Обозначим через



Крутильные моменты, действующие в сечениях вала, зависят от взаимного поворота двух смежных дисков и определяются формулами
на первом участке

на втором участке


на


Уравнения движения удобнее всего составлять прямым способом (рис. 26,б).

Число этих уравнений

Одним из решений системы (65) является

описывающее равномерное вращение вала и дисков как жёсткого целого.
Кроме того, возможно решение, описывающее упругие колебания системы

Подставляя (67) в (65), получим

Система уравнений (68) содержит


Если преобразовать систему (68) и рассматривать её как однородную систему линейных алгебраических уравнений относительно неизвестных амплитуд

Для иллюстрации сказанного запишем систему (68) в преобразованном виде при


Отсюда получим частотный определитель

и частотное уравнение

В общем случае степень частотного уравнения относительно


При












Далее производят повторный расчёт при новом значении


Расчёт повторяется до тех пор, пока не будет достигнут удовлетворительный результат в последнем уравнении.
При реализации метода удобнее всего использовать компактную табличную схему вычислений, основанную на соотношениях типа

которые получаются из уравнений (68) после сложения первых i уравнений системы. Соотношение (71) выражает равенство крутящего момента в сечении i-го участка вала (левая часть) сумме моментов сил инерции всех расположенных слева дисков (правая часть).
Задаваясь значением




Далее из того же соотношения для


Общая формула имеет вид

Процесс продолжается таким образом до



Вследствие неточности принятого исходного значения


После нескольких расчётов такого типа (при разных значениях


Рис. 27
Точки пересечения кривой с осью абсцисс соответствуют истинным значениям частот.
Объём вычислений может быть значительно уменьшен, если известны ориентировочные значения частот, для определения которых часто используют замену заданной системы упрощённой трехмассовой системой.
При записи решения (67) предполагалось, что колебания являются одночастотными, т.е. для любого диска описываются одной гармоникой

Существование спектра частот



где первый индекс у амплитуды означает номер диска, а второй индекс - номер соответствующей частоты.
Для получения общего решения необходимо также учесть возможность вращения всей системы как жёсткого целого (что соответствует частоте

добавить слагаемое вида (66), и тогда общее решение уравнений движения (65)


Уравнения (72) содержат 2n неизвестных:









Таким образом, для полного решения задачи необходимо и достаточно указать 2n начальных условий - угловые смещения и угловые скорости всех n дисков.
При произвольно заданных начальных условиях колебания каждого диска будут многочастотными, т.е. будут представлять собой сумму гармоник. Если начальные условия смещения соответствуют одной из собственных форм колебаний, то в дальнейшем процессе будут реализованы эта и только эта собственная форма и соответствующая собственная частота. В общем случае колебания будут носить сложный характер и представлять собой совокупность n форм колебаний. Относительное значение каждого из них зависит от близости заданной системы начальных смещений к той или иной собственной форме.
Маятник с колеблющейся точкой подвеса
Рассмотрим маятник (рис.61,а). Если точка подвеса неподвижна, то единственной силой, создающей момент относительно точки подвеса, является вес груза

Уравнение малых колебаний маятника имеет вид

Если же точка подвеса колеблется вдоль оси y по закону

то при составлении уравнения моментов нужно учесть переносную силу инерции



или


Рис. 61
Уравнение (160) можно привести к стандартному виду - уравнению Матье.
Для этого положим:

Теперь из диаграммы Айнса-Стретта видно, что параметр а не зависит от амплитуды колебаний точки подвеса и сколь бы малой ни была амплитуда



Рассмотрим вопрос об устойчивости верхнего положения маятника (рис.61,б). При неподвижной опоре это положение, конечно, неустойчиво; однако вибрации основания могут придать ему устойчивость. Для получения уравнения движения в данном случае достаточно изменить знак перед членом, содержащим ускорение



Из рис.61,в видно, что верхнее положение маятника может быть устойчивым. При небольших амплитудах колебаний




Метод Граммеля
Принимая форму колебаний подобной статическим прогибам системы от некоторой подходящей нагрузки, можно существенно увеличить точность расчёта за счёт исключения операции дифференцирования. Еще большая точность достигается в методе Граммеля, в котором дифференцирование заменяется интегрированием. Последовательность операций здесь такова:
1. Задают форму колебаний и вычисляют максимальную кинетическую энергию движения:

2. Определяют максимальные силы инерции:

3. Определяют внутренние силы в элементах системы, вызываемые нагрузками Fi.
4. По внутренним силам вычисляют максимальную потенциальную энергию деформации П0.
5. Из равенства Кmax = П0 определяют частоту колебаний.
Применим метод Граммеля для вычисления частоты колебаний консольной балки. Принимая x = (z/


Интенсивность сил инерции:

Поперечная сила в сечении:

Изгибающий момент:

Потенциальная энергия деформации:

Приравнивая Kmax = По, находим

что отличается от точного решения на 0,42 %.
Метод последовательных приближений
Докажем, что обычный процесс последовательных приближений приводит к первой собственной форме колебаний. Основой процесса является сравнение двух кривых аn и аn+1, из которых вторая получается как линия прогибов, вызванных нагрузкой man; при этом приближенное значение квадрата частоты определяется по формуле

Подобно выражению (265) представим исходную кривую


Тогда нагрузка, соответствующая прогибам


Рассмотрим одно из слагаемых этой нагрузки -







который отличается от ряда (282) тем, что каждый член ряда разделен на квадрат соответствующей частоты. Так как









Как видно, при

Поэтому может показаться, что попытка построить вторую собственную форму при помощи этого метода обречена на неудачу, так как всякое искажение, вносимое первой формой в приближенную вторую форму, будет постепенно увеличиваться; после большого числа построений второй тип колебаний совершенно исчезнет, и останется лишь первый тип.
Однако несколько видоизменяя метод, можно добиться того, что в результате последовательных приближений «очистится» не первая, а именно вторая собственная форма колебаний. Этот прием нашел практическое применение при расчете изгибных колебаний крыльев самолетов и лопаток турбин.
Прием основан на устранении формы


Допустим, что в разложении (281) отсутствует слагаемое, соответствующее первой форме, тогда оно не сможет возникнуть при всех последующих операциях, и ряд (284) принимает вид

При




где


Коэффициент




Подставляя сюда (285), получим

Далее от нагрузки





Однако первая собственная форма может быть известна лишь приближенно, поэтому операция, заключенная в (285), не гарантирует полного освобождения от первой формы



где коэффициент

функций



которое после подстановки (286) дает

Затем следует определить кривую



В таком процессе последовательных приближений ортогонализация сопровождает каждый шаг выкладок и, непрерывно вытесняя «примесь» первой формы, приведет ко второй собственной форме и второй частоте, которая, подобно (280), определится формулой

Таким же образом при помощи сопровождающей ортогонализации можно определить третью собственную форму и третью частоту и т.д.
Метод Ритца
Зададимся несколькими функциями f1(x) , f2(x) ,... , fn(x), каждая из которых удовлетворяет геометрическим граничным условиям задачи, и образум функцию f(x) как сумму
f(x) = C1f1(x) +C2f2(x)+...+Cnfn(x). (272)
Если эту функцию подставить в формулу Рэлея

то результат будет зависеть от конкретного выбора коэффициентов С1 , С2 , …, Сn.
Метод Ритца основан на простой идее: коэффициенты С1 , С2 , …, Сn должны быть выбраны так, чтобы вычисление по (273) дало наименьшее значение для w2. Из теоремы Рэлея вытекает, что такой выбор будет наилучшим (при данной системе функций fi).
Условия минимума w2 имеют вид

т.е.

Разделив это уравнение на интеграл


Уравнения (274) однородны и линейны относительно С1 , С2 , …, Сn и их число равно числу членов выражения (272). Приравнивая нулю определитель, составленный из коэффициентов при С1 , С2 , …, Сn, получим частотное уравнение. Это уравнение не только дает хорошее приближение для низшей частоты, но также определяет (хотя и с меньшей точностью) значения высших частот; при этом можно будет вычислить столько частот, сколько слагаемых принято в выражении (272).
Метод Ритца, как и метод Рэлея, позволяет решить задачу в случаях разрывных функций EJ и m и когда эти функции представлены различными аналитическими выражениями на различных участках.
Иногда та же идея используется в иной форме. Например, при исследовании поперечных колебаний турбинных лопаток задаются функцией f(x) = axs (начало координат в закрепленном конце). Применяя затем формулу Рэлея (273), получают частоту в виде зависимости от показателя степени s. Затем при помощи числовых расчетов определяют значение s, которому отвечает наименьшая частота. Это позволяет достаточно надежно определить как форму, так и частоту колебаний первого тона.
Пример 20. Определить методом Ритца низшую собственную частоту поперечных колебаний консоли переменного сечения, имеющей толщину, равную единице; высота изменяется по линейному закону:



(

Непосредственное решение
Для применения первого способа необходимо предварительно разложить периодические возмущающие моменты в ряды Фурье. После этого уравнения (139) решаются несколько раз - отдельно для каждой гармоники возмущения. Это приводит к ряду однотипных частных задач, каждая из которых требует анализа действия возмущающих моментов одинаковой частоты


При этом стационарные колебания будут происходить с частотой возмущения:

Подставляя (140) и (141) в (139), получим систему алгебраических уравнений

Решая эту систему, находим амплитуды вынужденных колебаний



Обратный способ
Отделяем грузы и рассматриваем упругий безмассовый скелет системы под действием кинетических реакций - сил инерции





пружины, равное её удлинению, можно записать в виде

Перемещение правого конца второй пружины


Из этих соотношений получим

Таким образом, совпали формы записей дифференциальных уравнений движения по основному (уравнения Лагранжа) и прямому способам, а уравнения, полученные обратным способом, отличаются от них по форме. Это связано с тем, что при нашем выборе обобщённых координат кинетическая энергия имеет каноническую форму:

т.е. не содержит произведений скоростей



то уравнения Лагранжа совпали бы с уравнениями, полученными обратным способом.
Сопоставляя полученные варианты записей по прямому и обратному способам, можно сделать следующее общее заключение: при составлении системы уравнений по прямому способу




Таким образом, пользуясь прямым способом, приходим в общем случае к системе:


а применяя обратный способ - к системе:


Принципиально важно, что специальным выбором обобщённых координат можно одновременно придать каноническую форму как кинетической, так и потенциальной энергии. Такие координаты




и уравнения Лагранжа принимают вид


Каждое из уравнений (35) интегрируется независимо от других. Иначе говоря, при использовании нормальных координат система представляет собой как бы совокупность независимых парциальных систем с одной степенью свободы.
Общее решение стандартного уравнения
Известны несколько методов решения уравнения (81). Рассмотрим наиболее часто используемый метод - метод вариации произвольных постоянных, применение которого позволяет получить результат, пригодный для любых законов изменения возмущающей силы.
Идея метода состоит в том, что частное решение уравнения (81) ищется в виде

соответствующем решению однородного уравнения, но здесь величины С1 и С2 следует считать не постоянными, а переменными. В результате задача определения функции x(t) заменяется задачей определения двух функций - C1(t) и C2(t). Так как для этого имеется только одно уравнение (82), то функции C1(t) и C2(t) можно связать еще одной произвольной зависимостью.
Составим выражение скорости:

и свяжем



тогда скорость запишется в форме

а ускорение

Подставляя (82) и (84) в (81), получим

Из (83) и (85) можно найти производные



Интегрируя, получим

где B1 и B2 - постоянные величины.
Подставляя (86) в ( 82), получим общее решение уравнения (81)

или, внося



Соответственно для скорости

Значения постоянных B1 и B2 можно определить только после того, как указаны начальные условия движения. Если


Тогда решение принимает вид

Здесь первые два слагаемых описывают свободные колебания, вызванные начальными возмущениями x0 и V0, а третье слагаемое характеризует вынужденные колебания, вызванные действием возмущающей силы F(t).
В случае нулевых начальных условий, когда движение начинается при x0 = 0 и V0 = 0,

В некоторых случаях удобнее использовать другую форму решения, которую получим, интегрируя по частям решение (89).
Положим

Тогда

Заменяя


Если в начальный момент времени F(0)=0, то решение принимает вид

где

Применим полученные результаты к случаю кинематического возбуждения колебаний (рис.37). Полагая F(t)=Cf(t), основное решение (89) запишем в виде

Аналогично вместо формулы (90) при F(0)=0 получим

Общие положения и примеры автоколебательных систем
Во всех рассмотренных ранее системах с неупругими сопротивлениями стационарные колебательные процессы оказывались возможными благодаря наличию внешних воздействий периодического характера. Однако в некоторых системах стационарные колебания возможны и без периодических воздействий извне; такие системы называются автоколебательными или самовозбуждающимися. Так как в любом реальном колебательном процессе неизбежно происходит рассеяние энергии, то всякая автоколебательная система обладает источником энергии, пополняющим все энергетические потери, но по своей природе источник не обладает колебательными свойствами.
Способность системы так регулировать отбор энергии от источника, чтобы появлялись автоколебания, определяется некоторыми ее свойствами. Этими свойствами являются динамические характеристики - собственные частоты и формы колебаний и коэффициенты затухания, определяющие «динамическую индивидуальность» системы.
Приведем несколько примеров возникновения автоколебаний. Во многих случаях самовозбуждение колебаний возникает вследствие взаимодействия системы с потоком жидкости, доставляющим энергию, необходимую для поддержания колебаний системы. Так, если деревянный стержень полукруглого сечения, подвешенный на пружинах, обдувать потоком воздуха, то стержень будет совершать колебания в вертикальной плоскости, перпендикулярной к направлению потока, причем с течением времени эти колебания становятся весьма интенсивными. Такой стержень полукруглого сечения хорошо моделирует условия реальной проблемы - «галопирование» линий электропередачи. При некоторых метеорологических условиях (главным образом при обледенении) провода линий электропередачи, протянутые между пилонами, могут колебаться с весьма большими амплитудами и низкими частотами.
Колебания стержня полукруглого сечения называют колебаниями системы с одной степенью свободы. Это означает, что движение совершается по одной форме, и соответствующее перемещение системы «стержень - пружины» можно охарактеризовать одной переменной величиной, например вертикальным отклонением центра тяжести стержня от своего среднего положения.
Возможен такой тип автоколебаний, которые могут существовать лишь в случае возбуждения более чем одной степени свободы. В этом случае все положения, которые принимает система в процессе колебаний, могут быть описаны лишь при помощи более чем одной переменной величины.
Примером такой системы являются автоколебания крыла самолета в воздушном потоке. Длинная гибкая опора позволяет крылу перемещаться вверх и вниз как жесткому целому (таким же образом движется и стержень полукруглого сечения); это движение соответствует первой степени свободы. Движение, соответствующее второй степени свободы, - это поворот крыла вокруг своей оси, сопровождающийся деформацией тонкой листовой пружинки; при таких колебаниях изменяется наклон крыла относительно набегающего потока. Система имеет и другие степени свободы (так, крыло может перемещаться параллельно потоку), но они не играют существенной роли. При достаточно высокой скорости потока крыло совершает вертикальные колебания, и одновременно происходят изменения угла наклона крыла относительно набегающего потока (угла атаки). Это пример классического флаттера-движения, происходящего с двумя степенями свободы.
Флаттер может возникать также у лопастей вертолетов и лопаток турбомашин. На практике явление флаттера служит объектом обширных исследований; условие отсутствия флаттера часто является одним из основных требований при проектировании.
Возникновение флаттера связано с выбором «формы флаттера», для которой выполняются определенные соотношения между амплитудами и фазами колебаний, соответствующих различным степеням свободы. Условие возникновения флаттера зависит от скорости потока, а также от плотности и температуры воздуха. Предположим, что скорость изменяется. От скорости потока зависит значение энергии, получаемой системой за один цикл колебаний, и значение энергии, рассеиваемой за цикл колебаний вследствие внутреннего и аэродинамического демпфирования. Когда отношение этих значений энергии становится равным единице, в системе могут установиться колебания постоянной амплитуды; соответствующая скорость самолета называется критической скоростью флаттера.
Каждой из возможных форм флаттера соответствует своя критическая скорость, и все расчеты флаттера проводятся с целью удостовериться, что наименьшая из критических скоростей с достаточным запасом превышает максимально возможную скорость полета самолета.
Существуют три пути борьбы с флаттером.
Первый способ основан на таком изменении характеристик системы, при котором достигается независимость колебаний, соответствующих различным степеням свободы, причем демпфирование всех этих различных форм колебаний положительно. Так, можно добиться того, чтобы поворот оси профиля крыла относительно продольной оси сечения слабо зависел от вертикального перемещения оси. Для этого нужно, чтобы ось занимала определенное положение, а распределение массы по сечению профиля удовлетворяло определенному условию. Другой способ заключается в увеличении собственных частот конструкции за счет увеличения отношений «жесткость/масса» отдельных ее частей. Этот способ основан на том, что энергия, получаемая системой при флаттере за один цикл колебаний, почти не зависит от частоты, тогда как энергия, рассеиваемая за один цикл, пропорциональна частоте.
Два рассмотренных метода обычно используются в практике самолетостроения. Третий метод борьбы с флаттером, вызываемым аэродинамическими силами, не всегда эффективен, но часто с успехом используется для устранения других видов автоколебаний. Этот метод заключается в демпфировании системы. Увеличивая трение в системе, склонной к флаттеру (т.е. увеличивая энергию, рассеиваемую за один цикл колебаний заданной амплитуды) можно, как правило, повысить критическую скорость системы.
Общие сведения о свободных колебаниях
Прежде чем перейти к строгому математическому описанию поведения различных систем при свободных колебаниях, остановимся подробно на природе их возникновения.
Известно, что в ряде случаев тело, получившее некоторое начальное возмущение, после удаления причины этого возмущения продолжает совершать колебания. Эти свободные колебания играют важнейшую роль не только в плане проверки системы на резонанс, т.е. на выявление совпадения одной из собственных частот колебаний с частотой действующих на систему постоянно вибрационных нагрузок. Дело в том, что поведение системы при свободных колебаниях характеризует её "динамическую индивидуальность", которая определяет поведение системы при всех других условиях.
Рассмотрим некоторые примеры возникновения свободных колебаний. После того как по струне рояля ударяет один из молоточков, струна некоторое время продолжает самостоятельно совершать колебания - свободные колебания. Это становится возможным, во-первых, потому, что струна имеет массу и при движении накапливает кинетическую энергию, а во-вторых, потому, что при отклонении от положения равновесия струна накапливает потенциальную энергию .
Точно так же обычный маятник может совершать колебания благодаря тому, что, во-первых, его гиря обладает массой и, во-вторых, при подъёме гири относительно своего низшего положения она накапливает потенциальную энергию.
Аналогично приведенным примерам корабли, летательные аппараты, здания, машины, люди и вообще все тела могут накапливать энергию за счёт изменения формы. Так как все тела обладают ещё и массой, то после тех или иных начальных толчков они могут совершать свободные колебания.
Идеальным объектом исследования свободных колебаний может служить подвешенная за один конец велосипедная цепь. Пусть свободно висящая цепь первоначально находится в состоянии покоя. Свободные колебания можно вызвать, если отклонить цепь каким-либо образом, а затем отпустить или резко её ударить (но так, чтобы боковое перемещение любой точки цепи было малым по сравнению с длиной цепи).
При этом можно наблюдать следующее:
1. Развитие движения во времени зависит от того, как оно началось.
2. Движение постепенно затухает.
3. При своем движении цепь не имеет какой-либо определённой формы; с течением времени форма цепи изменяется, однако в конце движения колебания часто характеризуются более или менее отчетливой формой.
4. Невозможно указать "частоту" колебаний, но с течением времени движение может принять определённую частоту.
Кажущийся хаотический характер колебаний можно упорядочить, если надлежащим образом задать начальные условия движения. В этом случае удаётся получить колебания цепи с неизменной формой и определённой частотой. Проще всего этого можно добиться следующим образом. Подвесим цепь к кулисному механизму (рис. 9).

Рис. 9
При вращении кривошипа точка подвеса перемещается в горизонтальном направлении по синусоидальному (т.е. гармоническому) закону. Если при этом регулировать скорость двигателя, приводящего механизм в движение, то можно изменять частоту колебаний точки подвеса. При очень низких частотах цепь будет просто перемещаться из стороны в сторону, сохраняя более или менее вертикальное положение. Однако при возрастании частоты наступает момент, когда цепь начинает интенсивно раскачиваться с частотой, равной частоте возбуждения (рис. 10,а). Эти колебания не являются свободными, так как цепь находится под действием вибрационной нагрузки. Но если внезапно остановить двигатель, т.е. удалить внешнюю нагрузку, то последующие колебания будут свободными и при этом совершенно не такими, как при случайно заданных начальных условиях. Эти колебания будут затухать, но всё время будут сохраняться форма и частота колебаний цепи. Иначе говоря, характер движения с течением времени остаётся неизменным. Можно показать, что существует целый ряд частот начального возбуждения, для каждой из которых характер движения будет иным, но также неизменным во времени.
Так, при постепенном увеличении частоты колебаний механизма можно возбудить колебания, во время которых цепь принимает форму, показанную на
рис. 10,б.
После резкой остановки точки подвеса такие колебания постепенно затухают, сохраняя при этом свою частоту и форму. При еще более высоких частотах можно получить другие формы колебаний (рис. 10,в,г).
Таким образом, цепь обладает рядом форм свободных колебаний, которые называются собственными формами. Каждой собственной форме соответствуют определённая частота и скорость затухания колебаний.
Собственные частоты системы (разумеется, любой системы, а не только подвешенной цепи), её собственные формы и скорости затухания являются индивидуальными характеристиками системы; они не связаны ни с какими внешними воздействиями.

Рис. 10
Экспериментальные исследования показывают, что увеличение массы системы приводит к снижению, а увеличение жёсткости - к возрастанию всех её собственных частот. При этом различные частоты изменяются в разной степени.
Собственные формы колебаний системы обладают следующими свойствами: любая возможная конфигурация системы может быть представлена в виде суперпозиции (наложения) некоторого числа таких конфигураций, каждая из которых соответствует одной собственной форме колебаний. Таким образом, если задать системе некоторую статическую деформацию, а затем освободить систему, то возникнут свободные колебания по всем соответствующим формам; каждое из таких колебаний будет происходить с соответствующей собственной частотой независимо от остальных движений. Любая комбинация двух собственных форм колебаний также является собственной формой.
Теперь перейдём к рассмотрению такой особенности свободных колебаний, как их затухание.
Эффект затухания колебаний объясняется наличием трения; иногда его называют демпфированием. Звук колокола слышен в течение длительного времени после удара, так как нет значительных сил трения, которые привели бы к рассеянию механической энергии за счёт её перехода в тепловую энергию, а рассеяние энергии за счёт излучения звуковых волн происходит весьма медленно.
С другой стороны, если раскачать кузов автомобиля, а затем отпустить его, то колебания быстро затухнут. Это объясняется действием специально установленных демпферов.
Рассеяние энергии имеет место в любой колебательной системе. Известно, например, что при вибрациях самолёта часть энергии рассеивается в панелях обшивки за счёт трения в заклёпочных соединениях. Значительным демпфированием должны обладать конструкции зданий, что очень важно с точки зрения поведения здания при землетрясении.
Иногда, если это особенно желательно, можно искусственно вводить трение; так, например, на автомобилях устанавливают демпферы колебаний. Прибор, стрелка которого безостановочно колеблется около положения, соответствующего истинному показанию, доставляет большое неудобство в работе. Поэтому, чтобы стрелка пришла в это положение достаточно быстро, вводится демпфирирование. Чрезмерно сильное трение является столь же вредным, как и недостаточное трение, поскольку в этом случае стрелка перемещается в положение отсчёта слишком медленно.
Существует много способов искусственного введения трения в систему. Это может быть осуществлено, например, электрическим способом, но чаще используются чисто механические методы демпфирования. Перечислим основные из них.
1. Вязкое трение в жидкости. Простейшим примером является гидравлический демпфер, который состоит из поршня, перемещающегося в цилиндре; трение возникает при перетекании жидкости (часто вместо жидкости используется воздух) в тонком зазоре между поршнем и стенкой цилиндра. В некоторых других устройствах используются лопасти, движущиеся в масле или силиконовой жидкости.
2. Материалы с высоким уровнем рассеяния энергии. При ударе по "колоколу", изготовленному из специального сплава меди и марганца, вместо звона слышится глухой стук. В амортизирующих опорах часто используют резину; это связано с её высокими демпфирующими характеристиками.
Лопатки компрессоров иногда изготавливают из волокнистых полимерных материалов, обладающих значительным внутренним трением.
3. Демпфирующие покрытия панелей. Существуют такие материалы, нанесение которых на поверхность металлических панелей приводит к тому, что при ударе по панели вместо характерного для металлов звука слышится глухой стук.
4. Сухое трение, возникающее при взаимном скольжении поверхностей в процессе вибрации. Этот способ используется, например, в некоторых компрессорах газовых турбин, где осуществлено шарнирное крепление лопаток к ротору. Кроме того, сухое трение возникает, когда в некоторые пружины с целью демпфирования вставляются пучки металлической проволоки.
5. Слоистые конструкции. Панели, состоящие из тонких металлических листов, разделённых тонким слоем вязкоупругого материала, обладают хорошими звукоизолирующими свойствами.
6. Пенопластовые или резиновые прокладки. Например, электрические лампочки, упакованные в такие прокладки, можно без всякого риска бросать с большой высоты на твёрдый пол.
Таким образом, существуют два вида демпфирования: искусственно вводимое и связанное с естественными силами трения. Если искусственно вводимое трение чаще всего допускает теоретическую оценку, то естественное трение, как правило, не поддается расчёту и должно определяться экспериментально.
Появление трения или его увеличение не приводит к заметным изменениям частоты и формы собственных колебаний. Поэтому исследование свободных колебаний вначале удобно проводить без учёта трения.
Общий случай
Способы решения. Если внешние силы изменяются по периодическому закону, то обычно их раскладывают в тригонометрический ряд, т.е. представляют в виде суммы гармоник. Затем на основании принципа независимости действия сил суммарное движение определяется как сумма движений, вызванных каждой из гармоник в отдельности. При таком подходе задача сводится к задаче о вынужденных колебаниях системы, вызываемых действием одной гармоники возмущения




Решение этой основной задачи чаще всего ведут одним из двух способов: непосредственного решения или разложения по собственным формам колебаний. Наибольшее распространение в расчётной практике получил второй способ. Помимо этого, иногда используется способ разложения по собственным формам колебаний при сохранении заданного вида периодических нагрузок, т.е. без разложения их на гармонические составляющие.
Особенности каждого из этих способов рассмотрим на примере простейшей двухмассовой системы (рис.48).
Непосредственное решение. Предполагая, что внешняя нагрузка разложена в тригонометрический ряд, исследуем движение системы, вызванное одной гармоникой возмущения. Силы, действующие на каждую массу, обозначим через


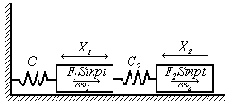
Рис. 48
Уравнения движения такой системы аналогичны уравнениям движения при свободных колебаниях, но нули в правых частях заменяются действующими силами



Решение этой системы, как и решение одного уравнения, состоит из двух частей: решения соответствующей однородной системы и частного решения неоднородной системы (122).
Слагаемое, описывающее колебания с собственной частотой (т.е. решение однородной системы), меняется с течением времени, быстро уменьшаясь вследствие действия сил затухания. Основной интерес представляет вторая часть решения, соответствующая незатухающему стационарному процессу вынужденных колебаний.
Примем частное решение в виде


После подстановки (123) в (122) получим два уравнения с двумя неизвестными амплитудами



Решая систему уравнений (124), находим

Знаменатели выражений для









При




При



При помощи (125) можно найти форму вынужденных колебаний, определяемую отношением





Эти силы можно представить в виде

а затем решать две задачи: действуют только «синусные» составляющие




В первой задаче получаются уравнения:

а во второй (когда частное решение имеет вид:



Решая каждую из этих задач и суммируя результаты, получим решение исходной задачи.
Если возмущающие силы имеют полигармоническую структуру

то резонанс становится возможным при








т.е. при совпадении любой из

Определение движения по начальным условиям
Если требуется определить движение, следующее после начального возмущения, то необходимо указать для всех точек балки как начальные смещения, так и начальные скорости:

и использовать свойство ортогональности собственных форм:


Общее решение (201) запишем так:

Скорость определяется выражением

Подставляя в правые части уравнений (211) и (212)

получим


Умножая эти выражения на


Бесконечные суммы в правых частях исчезли вследствие свойства ортогональности. Из (213) следуют формулы для постоянных



Теперь эти результаты нужно подставить в решение (211).
Снова подчеркнём, что выбор масштаба собственных форм несущественен. Если, например, в выражении собственной формы (209) принять вместо





Определение форм и частот колебаний
Для круглой пластины в уравнениях (317) для амплитудной функции



Таким образом, уравнение (317) в полярных координатах принимает форму

Решения этих уравнений, соответствующие колебаниям пластины с n
узловыми диаметрами, можно представить в виде

После подстановки этого выражения приходим к уравнениям:


Решениями уравнения (326) являются бесселевы функции порядка







Для кольцевой пластинки имеются четыре граничных условия (по два на каждом краю), которые образуют однородную систему уравнений относительно констант






В качестве примера рассмотрим колебания свободной сплошной круглой пластинки. В этом случае на контуре должны выполняться условия:

Изгибающий момент определяется формулой

Поперечная сила:

Крутящий момент:

Таким образом, граничные условия имеют вид


Учитывая, что





При подстановке в (329) вместо


учтем правила дифференцирования функций Бесселя:


В результате приходим к уравнениям


Здесь аргументом всех бесселевых функций является величина


Значения


Если ограничиться формами колебаний без узловых окружностей, то значениям


При


При


и соответствующая частота собственных колебаний

Для заделанной по контуру пластинки граничные условия

Частотное уравнение
