Автоматы для регулярных языков

Покажем, что каждый регулярный язык можно распознать конечным автоматом.

Теорема 5.1. Для каждого регулярного выражения r можно эффективно построить такой недетерминированный конечный автомат M, который распознает язык, задаваемый r, т.е. LM= Lr.

Доказательство Построение автомата M по выражению r проведем индукцией по длине r, т.е. по общему количеству символов алфавита ?, символов

и ?, знаков операций +, ?, * и скобок в записи r.

Базис. Автоматы для выражений длины 1:

, ? и a ? показаны на следующем рисунке.

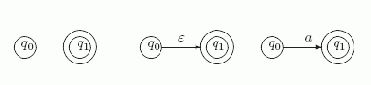
Рис. 5.1. 

Заметим, что у каждого из этих трех автоматов множество заключительных состояний состоит из одного состояния.

Индукционный шаг. Предположим теперь, что для каждого регулярного выражения длины

k построен соответствующий НКА, причем у него единственное заключительное состояние. Рассмотрим произвольное регулярное выражение r длины k+1. В зависимости от последней операции оно может иметь один из трех видов: (r1 + r2), (r1 r2) или (r1)*. Пусть M1= <?, Q1, q01, {qf1}, ?1 > и M2= <?, Q2, q02, {qf2}, ?2 > - это НКА, распознающие языки Lr1 и Lr2, соответственно. Не ограничивая общности, мы будем предполагать, что у них разные состояния: Q1 Q2 = .

Тогда НКА M= <?, Q, q0, {qf}, ? >, диаграмма которого представлена на рис. 5.2, распознает язык Lr =Lr1 + r2=Lr1

Lr2.

Рис. 5.2. 

У этого автомата множество состояний Q = Q1

Q2 { q0, qf}, где q0 - это новое начальное состояние, qf - новое (единственное !) заключительное состояние, а программа включает программы автоматов M1 и M2 и четыре новых команды ?-переходов: ? = ?1 ?2 {q0 q01, q0 q02, qf1 qf, qf2 qf}. Очевидно, что язык, распознаваемый НКА M, включает все слова из L{M1} и из L{M2}. С другой стороны, каждое слово w LM переводит q0 в qf, и после первого шага несущий его путь проходит через q01 или q02. Так как состояния M1 и M2 не пересекаются, то в первом случае этот путь может попасть в qf только по ?-переходу из qf1 и тогда w LM1}. Аналогично, во втором случае w LM2.

Для выражения r = r1? r2 диаграмма НКА M= <?, Q, q0, {qf}, ? >, распознающего язык Lr, представлена на следующем рисунке.

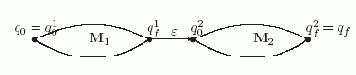
Рис. 5.3. 

У этого автомата множество состояний Q = Q1 Q2 , начальное состояние q0= q01, заключительное состояние qf =qf2, а программа включает программы автоматов M1 и M2 и одну новую команду - ?-переход из заключительного состояния M1

в начальное состояние M2, т.е. ? = ?1 ?2 { qf1 q02}. Здесь также очевидно, что всякий путь из q0= q01 в qf =qf2 проходит через ?-переход из qf1 в q02. Поэтому всякое слово, допускаемое M, представляет конкатенацию некоторого слова из LM1} с некоторым словом из LM2}, и любая конкатенация таких слов допускается. Следовательно, НКА M распознает язык Lr =L r1 ? r2}=L r1 Lr2.

Пусть r = r1*. Диаграмма НКА M= <?, Q, q0, {qf}, ? >, распознающего язык Lr=Lr1* = LM1*

представлена на рис. 5.3.


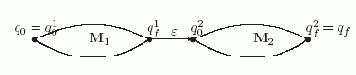
Рис. 5.3.  Диаграмма автомата M, распознающего язык Lr1*

У этого автомата множество состояний Q = Q1 { q0, qf}, где q0 - это новое начальное состояние, qf - новое (единственное !) заключительное состояние, а программа включает программу автомата M1 и четыре новых команды ?-переходов: ? = ?1 {q0 q01, q0 qf, qf1 q01, qf1 qf}. Очевидно, ? LM. Для непустого слова w по определению итерации w Lr1* для некоторого k 1 слово w можно разбить на k подслов: w=w1w2… wk и все wi LM1. Для каждого i= 1,… ,k слово wi переводит q01 в qf1. Тогда для слова w в диаграмме M имеется путь



Следовательно, w LM. Обратно, если некоторое слово переводит q0 в qf, то либо оно есть ? , либо его несет путь, который, перейдя из q0 в q01 и затем пройдя несколько раз по пути из q01 в qf1 и вернувшись из qf1 в q01 по ?-переходу, в конце концов из qf1 по ?-переходу завершается в qf. Поэтому такое слово w L M1*.

Из теорем 4.2 и 5.1 непосредственно получаем

Следствие 5.1.

Для каждого регулярного выражения можно эффективно построить детерминированный конечный автомат, который распознает язык, представляемый этим выражением.

Это утверждение - один из примеров теорем синтеза: по описанию задания (языка как регулярного выражения) эффективно строится программа (ДКА), его выполняющая.


Справедливо и обратное утверждение - теорема анализа.

Теорема 5.2.

По каждому детерминированному ( или недетерминированному) конечному автомату можно построить регулярное выражение, которое представляет язык, распознаваемый этим автоматом.

Доказательство этой теоремы достаточно техническое и выходит за рамки нашего курса.

Таким образом, можно сделать вывод, что класс конечно автоматных языков совпадает с классом регулярных языков. Далее мы будем называть его просто классом автоматных языков.

Автомат Mr, который строится в доказательстве теоремы 5.1 по регулярному выражению r, не всегда является самым простым.

Например, для реализации выражения-слова a1a2 … an, где ai ? (i=1,2, … , n), можно просто использовать автомат с (n+1) состоянием qi (i=0,1,2, … , n) и командами q{i-1} ai qi, в котором нет пустых ?-переходов, участвующих в общей конструкции для конкатенации. Также при построении автомата для объединения M1 и M2 можно сливать их начальные состояния в одно, если в них нет переходов из других состояний (тогда не потребуется новое начальное состояние). Можно также объединить их заключительные состояния, если из них нет переходов в другие состояния и алфавиты M1 и M2 совпадают. Если из заключительного состояния M1 нет переходов в другие состояния, то при конкатенации его можно объединить с начальным состоянием M2. Вместе с тем, утверждения задачи 5.9 показывают, что наша общая конструкция достаточно экономна.

Пример 5.7. Применим теорему 5.1 к регулярному выражению r = (1 +01 +001)*(? + 0 +00), которое, как мы заметили в примере 5.4, представляет язык, состоящий из всех слов, которые не содержат подслово '000'.

На рис. 5.5 представлены диаграммы автоматов M1 и M2, построенных по выражениям r1 = (1 +01 +001) и r2= (? + 0 +00), соответственно, с помощью конструкций для конкатенации и объединения. Как мы отмечали выше, автомат M1 можно было бы еще упростить, склеив начальные состояния q2, p1 и s1, а также заключительные состояния q3, p3 и s4.


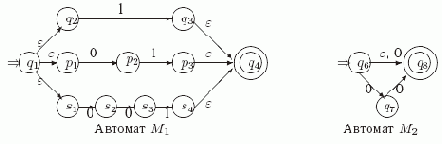
Рис. 5.5. 

Автомат M3 для выражения r1* = (1 +01 +001)* получается из M1 добавлением нового начального состояния q0 и заключительного состояния q5 и ?-переходов из q0 в q1 и q5, из q4 в q5 и из q5 в q1.Затем результирующий автомат для исходного выражения r получается последовательным соединением M3 и M2. Он представлен ниже на рис. 5.6.


Рис. 5.6. 

Регулярные выражения и языки

Регулярные выражения являются достаточно удобным средством для построения "алгебраических" описаний языков. Они строятся из элементарных выражений

, ?, a ? с помощью операций объединения (+), конкатенации (?) и итерации (*). Каждому такому выражению r соответствует представляемый им язык Lr. Смысл операции объединения языков мы знаем. Определим операции конкатенации и итерации (иногда ее называют замыканием Клини).

Пусть L1 и L2 - языки в алфавите ?.

Тогда L= L1 ? L2= { w | (

w1 L1) ( w2 L2) (w = w1w2)}, т.е. конкатенация языков состоит из конкатенаций всех слов первого языка со всеми словами второго языка. В частности, если ? L1, то L2 L, а если ? L2, то L1 L.

Введем обозначения для "степеней" языка L:

Таким образом в Li входят все слова, которые можно разбить на i подряд идущих слов из L.

Итерацию (L)* языка L образуют все слова которые можно разбить на несколько подряд идущих слов из L:

Ее можно представить с помощью степеней:

Часто удобно рассматривать "усеченную" итерацию языка, которая не содержит пустое слово, если его нет в языке:

. Это не новая операция, а просто удобное сокращение для выражения .

Отметим также, что если рассматривать алфавит ?={a1, … , am} как конечный язык, состоящий из однобуквенных слов, то введенное ранее обозначение ?* для множества всех слов, включая и пустое, в алфавите ? соответствует определению итерации ?^* этого языка.

В следующей таблице приведено формальное индуктивное определение регулярных выражений над алфавитом ? и представляемых ими языков.

Выражениеr ЯзыкLr

	L =
?	L_?={?}
a ?	La={a}
Пустьr1иr2-это	Lr1иLr2-представляемые
регулярные выражения.	ими языки.
Тогда следующие выражения
являются регулярными	и представляют языки:
r=(r1+r2)	Lr=Lr1 Lr2
r=(r1circr2)	Lr=Lr1?Lr2
r=(r1)*	Lr=Lr1*

При записи регулярных выражений будем опускать знак конкатенации ? и будем считать, что операция * имеет больший приоритет, чем конкатенация и +, а конкатенация - больший приоритет, чем +. Это позволит опустить многие скобки.

Например, (((1?0)?((1)*+0)) можно записать как 10(1* + 0).

Определение 5.1.

Два регулярных выражения r и p называются эквивалентными, если совпадают представляемые ими языки, т.е. Lr=Lp. В этом случае пишем r = p.

Нетрудно проверить, например, такие свойства регулярных операций:

r + p= p+ r (коммутативность объединения), (r+p) +q = r + (p+q) (ассоциативность объединения), (r p) q = r (p q) (ассоциативность конкатенации), (r*)* = r* (идемпотентность итерации), (r +p) q = rq + pq (дистрибутивность).

Пример 5.1.

Докажем в качестве примера не столь очевидное равенство: (r + p)* = (r*p*)*.

Пусть L1 - язык, представляемый его левой частью, а L2 - правой. Пустое слово ? принадлежит обоим языкам. Если непустое слово w L1, то по определению итерации оно представимо как конкатенация подслов, принадлежащих языку Lr Lp. Но этот язык является подмножеством языка L'=Lr*Lp* (почему?). Поэтому w L2 = (L')*. Обратно, если слово w L2, то оно представимо как конкатенация подслов, принадлежащих языку L'. Каждое из таких подслов v представимо в виде v= v11… vk1 v12… vl2, где для всех i=1, … , k подслово vi1 Lr и для всех j=1, … , l подслово vj2 Lp (возможно, что k или l равно 0). Но это значит, что w является конкатенацией подслов, каждое из которых принадлежит Lr Lp и, следовательно, w L1.

Рассмотрим несколько примеров регулярных выражений и представляемых ими языков.

Пример 5.2. Регулярное выражение (0 +1)* представляет множество всех слов в алфавите {0, 1}.

Пример 5.3. Регулярное выражение 11(0 +1)*001 представляет язык, состоящий из всех слов в алфавите {0, 1}, которые начинаются на '11', а заканчиваются на '001'.

Пример 5.4. Регулярное выражение (1 +01 +001)*(? + 0 +00) представляет язык, состоящий из всех слов в алфавите {0, 1}, которые не содержат подслово '000' ( см. задачу 5.3).

Пример 5.5. Регулярное выражение 1*(01*01*)* представляет язык L0ч, состоящий из всех слов в алфавите {0, 1}, в которых четное число нулей.

Действительно, каждое слово из L0ч либо вообще не содержит нулей, т.е.


входит в язык, представляющий 1*, либо может быть разбито на блоки вида 01i01j, i,j 0, которым, быть может, предшествует блок единиц. Выражение (01*01*), очевидно задает один такой блок, а его итерация - произвольную последовательность таких блоков.

Пример 5.6. Построим теперь регулярное выражение, представляющее язык L0ч1ч, который состоит из всех слов в алфавите {0, 1}, содержащих четное число нулей и четное число единиц.

Пусть w=w1w2 … wn - произвольное слово из L0ч1ч. Тогда, разумеется, n - четно, пусть n=2k. Разобьем w на пары соседних букв pi =w2i-1w2i, i= 1,2,… ,k. Возможны 4 вида таких пар: 00, 11, 01 и 10. Пар вида 00 и 11 может быть сколько угодно, а пар вида 01 и 10 обязательно четное число. Поэтому w разбивается на блоки, каждый из которых начинается одной из пар 01 или 10 и содержит еще одну такую пару. Каждый такой блок описывается выражением (01 +10)(00 + 11)*(01+10)(00 + 11)*. При этом перед первым блоком может быть префикс, состоящий из пар 00 и 11. Множество слов состоящих из пар 00 и 11 задается выражением (00 +11)*. Отсюда получаем выражение R0ч1ч, задающее язык L0ч1ч:

Определите конкатенацию для следующих пар

Задача 5.1.
Определите конкатенацию для следующих пар языков L1 и L2:
L1= {a, ab, abb} и L2= {?, a, b, ab, a}; L1= {?, a, ab, abb} и L2= { a, b, abb, a}; L1= {?, a, b, ab, aba} и L2= {?, a, b, ab, ba};
Задача 5.2. Пусть L={baa, bab, bba, bbb}. Какой из следующих языков является итерацией L* этого языка?
{ w | w=bw' и | w| делится на 3 } {?};{ w | w=bw' и | w| 3 } {?};{ w | w=w1w2w3 … w3n и w3i+1 = b для всех i <n } {?};{ w | w=bw' и | w| 12 }.
Задача 5.3. Докажите правильность регулярного выражения в примере 5.4.
Задача 5.4. Докажите следующие эквивалентности для регулярных выражений.
p*(p+q)* = (p + qp*)* = (p+q)*; p(qp)* = (pq)*p;(p*q*)* =(q*p*)*;(pq)+(q*p* + q*) = (pq)*p q+p*.
Задача 5.5. Постройте регулярное выражение, задающее язык язык L в алфавите ?= {0, 1}.
L= {w | w содержит нечетное число букв 0 и четное число букв 1}};L= {w | w содержит подслово 001 или подслово 110 };L= {w | w содержит по крайней мере мере два подряд идущих 0 };L= {w | w не содержит подслов 011 и 010}.
Задача 5.6. Определите, какой язык представляется следующими регулярными выражениями.
(0*1*)0; (01*)0; (00 +11 +(01 + 10)(00 +11)+(01+10))*.
Задача 5.7. Упростить следующие регулярные выражения.
(00*)0 + (00)*; (0+1)(? + 00)+ + (0+1); (0 + ?)0*1.
Задача 5.8. Выше в задаче 14.5 предлагалось построить автомат-распознаватель, который проверяет правильность сложения. Постройте регулярное выражение, задающее распознаваемый этим автоматом язык S, т.е. следующее множество слов в алфавите {0, 1}3
S= {(x1(1),x2(1),y(1)) (x1(2),x2(2),y(2)) … (x1(n),x2(n),y(n)) | y = y(n) … y(2)y(1) - это первые n битов суммы двоичных чисел x1= x1(n)… x1(2)x1(1) и x2 = x2(n)… x2(2)x2(1)}.
Задача 5.9. Пусть Mr - это автомат, который строится в доказательстве теоремы 5.1 по регулярному выражению r. Докажите, что
у Mr нет переходов из единственного заключительного состояния qf ; в диаграмме Mr из каждой вершины выходит не более двух ребер; число состояний Mr не более чем вдвое превосходит длину выражения r, т.е. |Q| 2 |r|.
Задача 5.10. Примените процедуру детерминизации из теоремы 4.2 и постройте ДКА, эквивалентный НКА из примера 5.7.

---

---