Основные определения

Одним из предшественников УБДР являются бинарные деревья решений.

Определение 3.1.

Бинарное дерево решений (БДР) - это бинарное дерево T=(V,E), все внутренние вершины которого помечены переменными, а листья - значениями 0 или 1. Из каждой внутренней вершины v выходят 2 ребра, одно помечено 0, другое - 1; вершина w0, в которую ведет ребро, помеченное 0, называется 0-сыном v, а вершина w1, в которую ведет ребро, помеченное 1, называется 1-сыном v.

Такое дерево, вершины которого помечены переменными x1, …, xn реализует булеву функцию f(x1, …, xn), если для каждого набора значений переменных ?1, ?2, …, ?n ветвь в дереве, соответствующая этому набору (из вершины xi идем по ребру, помеченному ?i), завершается листом с меткой f(?1, ?2, …, ?n).

Пример 3.1. Например, рассмотрим изображенное ниже БДР T1 (на всех рисунках предполагается, что ребра направлены сверху вниз).

Рис. 3.1. 

По определению T1 реализует функцию f1(x,y,z), представленную в таблице 3.1.

Таблица 3.1. Функция f1(x, y,z), реализуемая БДР T1 на рис.3.1

xyzf(x,y,z)

0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1.	1	0

Нетрудно построить ДНФ этой функции: f(x, y, z) = (¬ x

y) (¬ y z).

УБДР являются модификацией БДР, в которой все листья с одной меткой представлены одной вершиной, в каждую вершину может входить несколько ребер, возможен выбор порядка появления переменных на ветвях.

Определение 3.2. Пусть зафиксирован некоторый порядок n переменных

: x(1), …, x(n).

Упорядоченная бинарная диаграмма решений относительно порядка переменных

- это ориентированный граф без циклов с одним корнем, в котором

существует лишь две вершины, из которых не выходят ребра; они помечены константами 0 и 1 и называются стоками;остальные (внутренние) вершины помечены переменными и из каждой из них выходят два ребра, одно помечено 0, другое - 1;порядок, в котором переменные встречаются на любом пути из корня в сток, совместим с

, т.е. если из вершины, помеченной x(i), есть путь в вершину, помеченную x(j), то i < j.

Как и в случае БДР, УБДР реализует булеву функцию f(x1, …, xn), если для каждого набора значений переменных ?1, ?2, …, ?n путь в диаграмме, начинающийся в корне и соответствующий этому набору (из вершины xi идем по ребру, помеченному ?i), завершается стоком с меткой f(?1, ?2, …, ?n).

Из этого определения непосредственно следует, что каждая внутренняя вершина диаграммы v, помеченная переменной x(k), является корнем поддиаграммы, которая включает все вершины диаграммы, достижимые из v, и реализует некоторую функцию fv( x(k),x(k+1), …, x(n)) от (n -k +1) переменных x(k),x(k+1), …, x(n). При этом ее 0-сын w0 является корнем поддиаграммы, реализующей функцию fw0(x(k+1), …, x(n)) =fv( 0, x(k+1), …, x(n)), а 1-сын w1 - корень поддиаграммы, реализующей функцию fw1(x(k+1), …, x(n)) =fv( 1, x(k+1), …, x(n)). Пусть диаграмма реализует функцию f(x1, … , xn) = f'(x(1), …, x(n)) и ?(1),… , ?(k-1) - это набор значений переменных x(1), …, x(k-1), который соответствует пути из корня в вершину v (таких наборов может быть несколько). Тогда fv( x(k), …, x(n))= f'(?(1),… , ?(k-1),x(k), …, x(n)).

Пример 3.2. Реализуем с помощью УБДР функцию f1(x,y,z), представленную выше в примере 3.1, с помощью БДР T1 и таблицы 3.1.

Вначале зафиксируем порядок переменных: x < y < z. Объединив листья с одинаковыми метками и две z- вершины с одинаковыми потомками, получим УБДР D1, приведенную на рис.3.2.


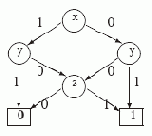
Рис. 3.2. 

Ясно, что реализация функции f1(x,y,z) с помощью УБДР D1 намного компактнее, чем с помощью БДР T1.

Под сложностью L(D) УБДР D будем понимать число внутренних вершин в D. Например, L(D1)=4. Может ли сложность диаграммы для некоторой функции зависеть от порядка переменных? Да! Рассмотрим порядок переменных y < x < z. Как показывает следующий рисунок, относительно этого порядка функцию f(x,y,z) можно реализовать УБДР D2 со сложностью L(D2)=3.


Рис. 3.3. 

Построение сокращенных УБДР по формулам

Алгоритм СОКРАЩЕНИЕ-УБДР позволяет построить сокращенную УБДР для функции f, по любой другой ее УБДР. Но как построить УБДР, если f задана, например, с помощью формулы? Можно, конечно, попытаться построить полное бинарное дерево решений, объединить в нем все листья с меткой 0 в один сток, а листья с меткой 1 - в другой. Затем применить к получившейся УБДР алгоритм СОКРАЩЕНИЕ-УБДР. Но этот подход годится только для функций от небольшого числа переменных, так как полное БДР для f(x1, …, xn) будет содержать 2n листьев.

Другой подход связан с построением УБДР "сверху-вниз". Объясним его для естественного порядка переменных: x1< x2 < … < xn.

Начнем построение с корня, помеченного x1. Рассмотрим две остаточные функции: f0(x1, …, xn)=f(0, x2, …, xn) и f1(x2, …, xn)=f(1, x2, …, xn). Если они одинаковы, то f не зависит от x1 и тогда изменим метку у корня на x2. Если обе функции f0 и f1 существенно зависят от x2, то для каждой из них добавляем вершину, помеченную x2, и далее реализуем по индукции. Если fk (k

{0, 1}) не зависит от переменных x2,… , xj, но зависит существенно от xj+1, то добавляем вершину, помеченную xj+1, и проводим в нее ребро с меткой k из вершины, соответствующей f . Пусть для некоторого i уже построены вершины для всех различных остаточных функций вида f?1 … ?i}(xi+1, … , xn)= f(?1… ?i, xi+1, … , xn), существенно зависящих от xi. Для каждой из них получим две остаточные функции f_{?1… ?i 0}( xi+2, … , xn)= f(?1… ?i, 0, xi+2, … , xn) и f_{?1… ?i 1}( xi+2, … , xn)= f(?1… ?i, 1, xi+2, … , xn). Затем выберем из множества этих функций разные, для каждой из них добавим в диаграмму вершину, помеченную xi+1, и проведем в них соответствующие ребра из вершин, помеченных x_{i}. Продолжая построение, дойдем до функций от 1-ой переменной xn и до констант, для которых минимальные реализации очевидны.

Пример 3.2. Рассмотрим, например, функцию f(x1, x2, x3, x4), заданную формулой (x1

x2 x4) (¬ x1 x2 ¬ x4) (¬ x2 x3) (¬ x2 x4), и построим для нее УБДР относительно порядка x1 < x2 < x3 <x4, используя описанную выше процедуру.

Вначале создадим корень, помеченный x1, и рассмотрим остаточные функции, получающиеся при x1=0 и x1 =1. Имеем



Они разные и обе существенно зависят от x2. Поэтому добавим для каждой из них вершину, помеченную x2. Затем для каждой из них определим остаточные функции, получающиеся при x2=0 и x2 =1. Получим



Так как f00=f10, а f01 и f11 от x3 не зависят, то нам потребуется только одна вершина, помеченая x3. Она будет представлять функцию f00=f10=(x3 x4). При x3=0 она превращается в x4, а при x3=1 равна константе 1. В результате получается УБДР Df, показанная на рис.3.6.


Рис. 3.6. 

Сокращенные УБДР

Когда порядок переменных зафиксирован, то достаточно просто можно по произвольной УБДР для функции построить минимальную УБДР, реализующую данную функцию.

Определение 3.3. УБДР называется сокращенной, если

из любой внутренней вершины v ее 0-сын и 1-сын не совпадают;нет такой пары внутренних вершин u и v, для которых поддиаграммы с корнями u и v являются изоморфными (т.е. взаимно однозначно отображаются друг на друга с сохранением всех меток).

Смысл этого определения понятен: если из некоторой вершины v оба ребра ведут в одну вершину, то такая вершина v не нужна, а если имеются две вершины с одинаковыми поддиаграммами, то их можно слить. Определим два типа эквивалентных преобразований УБДР.

Правило сокращения: если 0-сын и 1-сын вершины v совпадают и равны w, то удалить v, перенаправив все входящие в нее ребра в вершину w.

Правило слияния: если вершины v и w помечены одной переменной и имеют одинаковых 0-сыновей и 1-сыновей, то удалить вершину v, перенаправив все входящие в нее ребра в вершину w.

На следующем рисунке показаны преобразования по этим правилам.

Рис. 3.4.  Правило сокращения Правило слияния

Следующая простая теорема показывает, что применимость этих двух правил является критерием несокращаемости УБДР.

Теорема 3.1.

УБДР D является сокращенной тогда и только тогда, когда к ней не применимо ни правило слияния, ни правило сокращения.

Доказательство.

Если к D применимо правило сокращения, то не выполнено условие (1) из определения сокращенной УБДР, а если к D применимо правило слияния, то поддиаграммы с корнями v и w являются изоморфными и не выполнено условие (2).

? Пусть к УБДР D нельзя применить правило сокращения. Тогда в ней нет вершин с совпадающими 0- и 1-сыновьями и выполнено условие (1). Пусть к УБДР D нельзя применить правило слияния. Тогда из следующей леммы можно заключить, что в D нет пары вершин, поддиаграммы которых являются изоморфными, и следовательно, выполнено условие (2).

Лемма 3.2. Если в D есть такая пара вершин u и v, для которых поддиаграммы с корнями v и w являются изоморфными, то в D имеется и пара вершин v', w' с попарно одинаковыми 0- и 1-сыновьями и, следовательно, к D применимо правило слияния.

Доказательство леммы проведем индукцией по высоте h поддиаграмм Dv и Dw с корнями v и w, соответственно (так как Dv и Dw изоморфны, то их высоты, т.е. длины максимальных путей из корней до стоков, одинаковы).

Базис: h=1. В этом случае 0- и 1-сыновьями вершин v и w являются одинаковые стоки.

Шаг индукции. Предположим, что утверждение верно для h=k. Пусть Dv и Dw - поддиаграммы высоты h=k+1. Пусть v0 и w0 - это 0-сыновья вершин v и w, соответственно, а v1 и w1 - их 1-сыновья. Если v0=w0 и v1=w1, то в качестве v', w' подходят сами v и w. Если же для некоторого i {0,1} vi wi, то поддиаграммы и с корнями vi и wi являются изоморфными и имеют высоту k. Тогда по предположению индукции утверждение леммы выполнено.

Из теоремы 3.1 непосредственно следует, что, применяя к произвольной УБДР правила сокращения и слияния, мы, в конце концов, получим сокращенную УБДР. Чтобы эта процедура работала эффективо, нужно применять правила в порядке "снизу-вверх". Мы опишем этот алгоритм для "естественного" порядка переменных: x1, … , xn.

Алгоритм СОКРАЩЕНИЕ-УБДР

Вход: УБДР D для функции f(x1, … , xn).

Выход: сокращенная УБДР для .

1. Занумеруем множество вершин D: V = {v1, v2, …, vm}; 2. ДЛЯ i = n, n-1, …, 1 ВЫПОЛНЯТЬ 3. { 4. V(i) = { v | v помечена переменной xi }; /* Применение правила сокращения: 5. ДЛЯ КАЖДОЙ v V(i) ВЫПОЛНЯТЬ 6. ЕСЛИ (0-сын v) = (1-сын v) = w ТО} 7. { удалить v из V(i); 8. перенаправить все ребра, входящие в v, в вершину w; 9. удалить v из D } 10. ИНАЧЕ key(v) = (j, k), где vj - это 0-сын v, а vk - 1-сын v; /* Применение правила слияния: 11. Отсортировать V(i) по ключу key(v): пусть в этом порядке V(i)={ u1, …, uki}; 12. тек_ключ=(0, 0); 13. ДЛЯ j = 1, …, ki ВЫПОЛНЯТЬ 14. ЕСЛИ тек_ключ=key(uj) ТО 15. { удалить uj из V(i); 16. перенаправить все ребра, входящие в uj, в тек_вершина; 17. удалить uj из D } 18. ИНАЧЕ} {тек_вершина= uj; тек_ключ=key(uj)} 19. }

Пример 3.1. Рассмотрим пример применения алгоритма СОКРАЩЕНИЕ-УБДР, показанный на следующем рисунке.




Рис. 3.5.  Применение алгоритма СОКРАЩЕНИЕ-УБДР

На исходной УБДР слева все вершины уже занумерованы. Стрелки разделяют УБДР, получаемые после очередных итераций основного цикла в строках 2 - 19. При первом исполнении цикла i=3, V(3) = {v3}. Для вершины v3 условие в строке 6 выполнено (w= v6), поэтому применяется правило сокращения и эта вершина удаляется, а ее входы направляются в v6. При следующем исполнении цикла i=2, V(2) = {v2, v4}. После цикла в строках 5 - 10 key(v2)= {5, 6} и key(v4)= {5, 6}. После сортировки u1=v2, u2 = v4. В цикле в строках 13-18 для u2 выполнено условие в строке 14. Поэтому применяется правило слияния и вершина v4 удаляется, а ее вход передаeтся вершине v2. При третьем исполнении цикла i=1, V(1) = {v1}. Для вершины v1 условие в строке 6 выполнено (w= v2), поэтому применяется правило сокращения и эта вершина удаляется.

Оказывается, что построенная алгоритмом УБДР является единственной и минимальной для заданного порядка.

Теорема 3.2.

Алгоритм СОКРАЩЕНИЕ-УБДР строит сокращенную УБДР, эквивалентную исходной УБДР D.Эта сокращенная УБДР является при данном порядке переменных единственной (с точностью до изоморфизма) и минимальной.

Доказательство первого пункта непосредственно следует из выполнения критерия теоремы 3.1, так как к результирующей диаграмме никакое правило сокращения или слияния неприменимо.

Доказательство второго пункта основано на следующем индуктивном утверждении:

Лемма 3.1.

После выполнения i-ой итерации алгоритма в полученной диаграмме для каждой подфункции f(?1, ?2, …, ?_{i-1},xi, …, xn) (?k {0, 1} при k=1,2,…, i-1), существенно зависящей от xi, имеется ровно одна вершина - корень поддиаграммы, реализующей эту подфункцию.

Напомним, что функция f(x1, x2, …, xi, …, xn) существенно зависит от переменной xi, если существуют такие два набора значений аргументов (?1, …, ?i-1, 0, ?i+1,…, ?n) и (?1, …, ?i-1, 1, ?i+1,…, ?n), различающиеся только значением xi, на которых f принимает разные значения: f(?1, …, ?i-1, 0,?i+1, …, ?n) f(?1, …, ?i-1, 1,?i+1, …, ?n) .

Доказательство этой леммы и вывод из нее утверждения 2 теоремы 3.2 оставляем в качестве задач 3.2 и 3.3.



Задача 3.1. Докажите, что совершенная, сокращенная и минимальная ДНФ функции odd(X1,X2,…, Xn) совпадают и состоят из 2n-1 элементарных конъюнкций длины n.
Задача 3.2. Докажите лемму 3.2 возвратной индукцией по i.
Задача 3.3. Используя лемму 3.2, докажите утверждение 2 теоремы 3.2.
Задача 3.4. Постройте минимальные УБДР для двуместных функций: x y, x y, x + y, x y, x|y.
Задача 3.5. Постройте минимальные УБДР для функции

относительно двух упорядочений переменных:
x1 < x2 < x3 < x4 < x5 < x6 и x1 < x3 < x5 < x2 < x4 < x6.
Задача 3.6. Пороговая функция Tnk от n переменных с порогом k выдает 1, если во входном наборе имеется не менее k единиц: Tnk(x1,x2, …, xn) = 1 x1 + x2 + … + xn k.
Постройте минимальные УБДР для пороговых функций T32, T42, T53.Зависит ли сложность минимальной УБДР для пороговых функций от порядка переменных?Оцените сложность минимальной УБДР для пороговой функции Tnk.
Задача 3.7. Выберите подходящий порядок переменных и постройте для него минимальные УБДР, реализующие функции из задач 12.5 и 12.6.
Задача 3.8. Как мы видели, логические схемы естественным образом реализуются в виде неветвящихся программ. Наоборот, для деревьев решений и УБДР естественным программным представлением являются ветвящиеся программы, включающие лишь условные операторы вида if ... then ... else ... с тестами вида "x = 0?" и "x = 1?" (они соответствуют внутренним вершинам диаграмм) и операторы присвоения значения 0 или 1 результату (они соответствуют вершинам-стокам).
Напишите ветвящиеся программы, вычисляющие функции, представляемые УБДР D2 на рис. 3.3 и Df на рис.3.6.

---

---