Перечисляемый

Перечисляемый тип определяется конечным набором значений, представленных списком идентификаторов в объявлении типа. Значениям из этого набора присваиваются номера в соответствии с той последовательностью, в которой перечислены идентификаторы. Формат

объявления перечисляемого типа таков:

TYPE<имя> = (<список>);

<список>:= <идентификатор>,[<список>]

Если идентификатор указан в списке значений перечисляемого типа, он считается именем константы, определенной в том блоке, где объявлен перечисляемый тип. Порядковые номера значений в объявлении перечисляемого типа определяются  их позициями в списке идентификаторов, причем у первой константы в списке порядковый номер равен нулю. К данным перечисляемого типа относится, например, набор цветов:

TYPE <Цвет> = (Красный, Зеленый, Синий)

Операции те же, что и для символьного типа.

Переупорядочение путем перестановки в начало списка

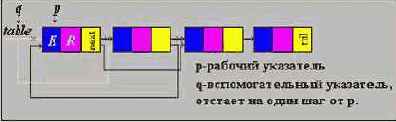
Найденный элемент сразу оказывается в голове списка.

Первоначально указатель q нулевой, указатель p указывает на начало списка; p перемещается на второй элемент, а q на первый. Указатель начала списка (table) перемещается на второй элемент, а указатель второго элемента на третий. Таким образом второй элемент перемещается на первое место.

(ПСЕВДОКОД)

   q=nil             

   p=table               

   WHILE (p <> nil) do   

     IF  key=k(p)

               then  SEARCH=p

               next(q)=next(p)

               next(p)=q

               table=p

               return

     end  IF

     q=p

     p=next(p)

   end WHILE

   SEARCH=0

   return

Переупорядочивание таблицы поиска путем перестановки найденного элемента в начало списка

Суть этого метода заключается в том, что элемент списка с ключом, равным заданному, становится первым элементом списка, а все остальные сдвигаются.

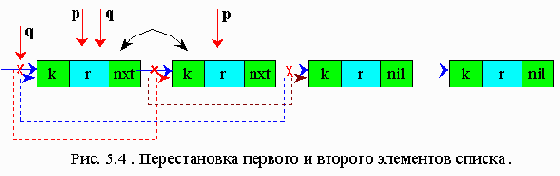
Этот алгоритм применим как для списков, так и для массивов. Однако не рекомендуется применять его для массивов, так как на перестановку элементов массива затрачивается гораздо больше времени, чем на перестановку указателей.

Алгоритм переупорядочивания в начало списка:

Псевдокод: q=nil p=table while (p <> nil) do   if key = k(p) then         if q = nil then    'перестановка не нужна'                  search = p               return         endif     nxt(q) = nxt(p)     nxt(p) = table     table = p     search = p     return   endif   q = p   p = nxt(p) endwhile search = nil return

Паскаль: q:=nil; p:=table; while (p <> nil) do   begin     if key = p^.k then       begin if q = nil       then 'перестановка не нужна'         search := p;  exit;  end;         q^.nxt := p^.nxt;         p^.nxt := table;         table := p;         exit;       end;     q := p;     p := p^.nxt;   end; search := nil; exit;

 

Поиск

Поиск является одной из основных операций при обработке информации в ЭВМ. Ее назначение - по заданному аргументу найти среди массива данных те данные, которые соответствуют этому аргументу.

Набор данных (любых) будем называть таблицей или файлом. Любое данное (или элемент структуры) отличается каким-то признаком от других данных. Этот признак называется ключом. Ключ может быть уникальным, т. е. в таблице существует только одно данное с этим ключом. Такой уникальный ключ называется первичным. Вторичный ключ в одной таблице может повторяться, но по нему тоже можно организовать поиск. Ключи данных могут быть собраны в одном месте (в другой таблице) или представлять собой запись, в которой одно из полей - это ключ. Ключи, которые выделены из таблицы данных и организованы в свой файл, называются внешними ключами. Если ключ находится в записи, то он называется внутренним.

Поиском по заданному аргументу называется алгоритм, определяющий соответствие ключа с заданным аргументом. Результатом работы алгоритма поиска может быть нахождение этого данного или отсутствие его в таблице. В случае отсутствия данного возможны две операции:

1. индикация того, что данного нет

2. вставка данного в таблицу.

Пусть k - массив ключей. Для каждого k(i) существует r(i) - данное. Key - аргумент поиска. Ему соответствует информационная запись rec. В зависимости от того, какова структура данных в таблице, различают несколько видов поиска.

Поиск делением пополам (двоичный поиск).

Совершенно очевидно, что других способов убыстрения поиска не существует, если, конечно, нет еще какой-либо информации о данных, среди которых идет поиск. Хорошо известно, что поиск можно сделать значительно более эффективным, если данные будут упорядочены. Вообразите себе телефонный справочник, в котором фамилии не будут расположены по порядку. Это нечто совершенно бесполезное! Поэтому мы приводим алгоритм, основанный на знании того, что массив а упорядочен, т.е. удовлетворяет условию

Ak : 1£ k < N : ak-1 ¹ ak

Основная идея - выбрать случайно некоторый элемент, предположим am, и сравнить его с аргументом поиска x. Если он равен x, то поиск заканчивается, если он меньше x, то мы заключаем, что все элементы с индексами, меньшими или равными m, можно исключить из дальнейшего поиска; если же он больше x, то исключаются индексы больше и равные m. Это соображение приводит нас к следующему алгоритму (он называется "поиском делением пополам"). Здесь две индексные переменные L и R отмечают соответственно левый и правый конец секции массива а, где еще может быть обнаружен требуемый элемент.

L := 0;

R := N-1;

found := FALSE;

WHILE (L Ј R) AND NOT found DO

    m := любое значение между L и R;

    IF a[m] = x THEN found := TRUE;

    IF a[m] < x THEN L := m+1

    ELSE R := m-1;

    END;

END;

Инвариант цикла, т.е. условие, выполняющееся перед каждым шагом, таков:

(L £ R) AND (Ak

: 0 £ k < L : ak < x) AND (Ak

: R < k < N : ak > x)

из чего выводится результат

found OR ((L > R) AND (Ak : 0 £ k < L : ak

< x) AND (Ak : R < k < N : ak > x))

откуда следует

(am = x) OR (Ak : 0 £ k < N : ak ¹ x)

Выбор m совершенно произволен в том смысле, что корректность алгоритма от него не зависит. Однако на его эффективность выбор влияет. Ясно, что наша задача - исключить на каждом шагу из дальнейшего поиска, каким бы ни был результат сравнения, как можно больше элементов. Оптимальным решением будет выбор среднего элемента, так как при этом в любом случае будет исключаться половина массива.
В результате максимальное число сравнений равно log N, округленному до ближайшего целого. Таким образом, приведенный алгоритм существенно выигрывает по сравнению с линейным поиском, ведь там ожидаемое число сравнений - N/2.

Эффективность можно несколько улучшить, поменяв местами заголовки условных операторов. Проверку на равенство можно выполнять во вторую очередь, так как она встречается лишь единожды и приводит к окончанию работы. Но более существенно следующее соображение: нельзя ли, как и при линейном поиске, отыскать такое решение, которое опять бы упростило условие окончания. И мы действительно находим такой быстрый алгоритм, как только отказываемся от наивного желания кончить поиск при фиксации совпадения. На первый взгляд это кажется странным, однако при внимательном рассмотрении обнаруживается, что выигрыш в эффективности на каждом шаге превосходит потери от сравнения с несколькими дополнительными элементами. Напомним, что число шагов в худшем случае - log N. Быстрый алгоритм основан на следующем инварианте:

(Ak : 0 £ k < L : ak < x) AND (Ak : R £ k < N : ak ³ x)

причем поиск продолжается до тех пор, пока обе секции не "накроют" массив целиком.

L := 0;

R := N;

  WHILE L < R DO

    m := (L+R) DIV 2;

    IF a[k] < x THEN L := m+1

    ELSE R := m ;

  END

END

Условие окончания - L і R, но достижимо ли оно? Для доказательства этого нам необходимо показать, что при всех обстоятельствах разность R-L на каждом шаге убывает. В начале каждого шага L < R. Для среднего арифметического m справедливо условие L Ј m < R. Следовательно, разность действительно убывает, ведь либо L увеличивается при присваивании ему значения m+1, либо R уменьшается при присваивании значения m. При L = R повторение цикла заканчивается. Однако наш инвариант и условие L = R еще не свидетельствуют о совпадении. Конечно, при R = N никаких совпадений нет. В других же случаях мы должны учитывать, что элемент а[R] в сравнениях никогда не участвует.Следовательно, необходима дополнительная проверка на равенство а[R] = x. В отличие от первого нашего решения приведенный алгоритм, как и в случае линейного поиска, находит совпадающий элемент с наименьшим индексом.

Поиск по бинарному дереву

Назначение его в том, чтобы по заданному ключу осуществить поиск узла дерева. Длительность операции зависит от структуры дерева. Действительно, дерево может быть вырождено в однонаправленный список, как правое на рис. 5.8.

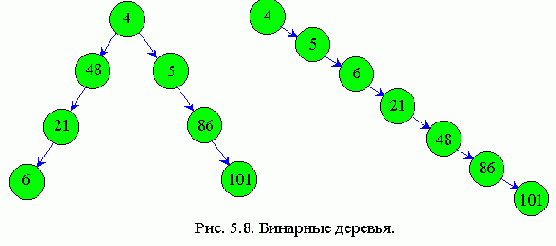
В этом случае время поиска будет такое же, как и в однонаправленном списке, т.е. придется перебирать N/2 элементов.

Наибольшего эффекта использования дерева достигается в том случае, когда дерево сбалансировано.В этом случае для поиска придотся перебрать не больше log2N

элементов.

Строго сбалансированное дерево - это дерево, в котором каждый узел имеет левое и правое поддеревья, отличающиеся по уровню не более, чем на единицу.

Поиск элемента в бинарном дереве называется бинарным поиском по дереву.

Такое дерево называют деревом бинарного поиска.

Суть поиска заключается в следующем. Анализируем вершину очередного поддерева. Если ключ меньше информационного поля вершины, то анализируем левое поддерево, больше - правое.

Пусть задан аргумент key

p = tree whlie p <> nil do   if key = k(p) then     search = p     return   endif   if key < k(p) then     p = left(p)   else     p = right(p)   endif endwhile search = nil return

p := tree; whlie p <> nil do   begin     if key = p^.k then       begin         search := p;         exit;       end;     if key < p^.k then       p := p^.left     else       p := p^.right;   end; search := nil;

Поиск с удалением

Удаление узла не должно нарушить упорядоченности дерева. Возможны три варианта:

1) Найденный узел является листом. Тогда он просто удаляется и все.

2) Найденный узел имеет только одного сына. Тогда сын перемещается на место отца.

3) У удаляемого узла два сына. В этом случае нужно найти подходящее звено поддерева, которое можно было бы вставить на место удаляемого. Такое звено всегда существует:

 - это либо самый правый элемент левого поддерева (для достижения этого звена необходимо перейти в следующую вершину по левой ветви, а затем переходить в очередные вершины только по правой ветви до тех пор, пока очередная ссылка не будет равна NIL.

- либо самый левый элемент правого поддерева (для достижения этого звена необходимо перейти в следующую вершину по правой ветви, а затем переходить в очередные вершины только по левой ветви до тех пор, пока очередная ссылка не будет равна NIL

Предшественником удаляемого узла называют самый правый узел левого поддерева (для 12 - 11). Преемником - самый левый узел правого поддерева (для 12 - 13).

Будем разрабатывать алгоритм для преемника (рис.5.9).

p - рабочий указатель;

q - отстает от р на один шаг;

v - указывает на приемника удаляемого узла;

t - отстает от v на один шаг;

s - на один шаг впереди v (указывает на левого сына или пустое место).

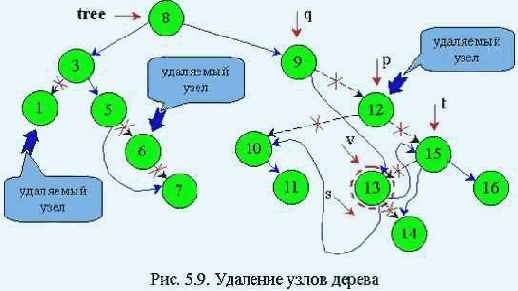
На узел 13 в конечном итоге должен указывать v, а указатель s - на пустое место (как  показано на рис. 5.9).

Псевдокод:  q = nil  p = tree while (p <> nil) and (k(p) <> key) do   q = p   if key < k(p) then     p = left(p)   else     p = right(p)   endif endwhile if p = nil then ‘Ключ не найден’                       return endif if left(p) = nil then  v = right(p)                      else if right(p) = nil                                then v = left(p)                                else ‘У nod(p) - два сына’ ‘Введем два указателя (t отстает от v на 1 ‘шаг, s - опережает)      t = p      v = right(p)      s = left(v)      while s <> nil do        t = v        v = s        s = left(v)      endwhile      if t <> p then        ‘v не является сыном p’        left(t) = right(v)        right(v) = right(p)      endif      left(v) = left(p)   endif endif if q = nil then ‘p - корень’                        tree = v               else  if p = left(q)                          then left(q) = v                          else right(q) = v                        endif endif freenode(p) return

Паскаль:   q := nil;    p := tree; while (p <> nil) and (p^.k <> key) do   begin     q := p;     if key < p^.k then       p := p^.left     else p := p^.right;   end; if p = nil then   WriteLn(‘Ключ не найден’);                  exit; end; if p^.left = nil then   v := p^.right else   if p^.right = nil then     v := p^.left   else     begin {Введем два указателя (t отстает от v на 1 шаг, s - опережает)}       t := p;       v := p^.right;       s := v^.left;       while s <> nil do         begin           t := v;           v := s;           s := v^.left;         end;       if t <> p then         begin     WriteLn(‘v не является сыном p’);           t^.left := v^.right;           v^.right := p^.right;         end;       v^.left := p^.left;       end;       end;       if p = q^.left then         q^.left := v       else         q^.right := v;      end; dispose(p);   end;

<
Контрольные вопросы

        1.        В чем состоит назначение поиска ?

        2.        Что такое уникальный ключ ?

        3.        Какая операция производится в случае отсутствия заданного ключа в списке ?

        4.        В чем разница между  последовательным  и  индексно-последовательным поиском ?

        5.        Какой из них более эффективный и почему ?

        6.        Какие способы переупорядочивания таблицы вы знаете ?

        7.        Основные отличия метода перестановки в начало от метода транспозиции .

        8.        Где они будут работать быстрее, в массиве или списке ?

        9.        В каких списках они работают, упорядоченных или нет ?

     10.     В чем суть бинарного поиска?

     11.     Как можно обойти бинарное дерево?

     12.     Можно ли применять бинарный поиск к массивам ?

     13.     Если удалить корень в непустом бинарном дереве, какой элемент станет на его место ?

Поиск со вставкой (с включением)

Для вставки элемента в дерево, сначало нужно осуществить поиск в дереве по заданному ключу. Если такой ключ имеется, то программа завершается, если нет, то происходит вставка.

Для включения новой записи в дерево, прежде всего нужно найти тот узел, к которому можно присоединить новый элемент. Алгоритм поиска нужного узла тот же самый, что и при поиске узла с заданным ключом. Однако непосредственно использовать процедуру поиска нельзя, потому что по ее окончании не фиксирует тот узел, из которого была выбрана ссылка NIL (search = nil).

Модифицируем описание процедуры поиска так, чтобы в качестве ее побочного эффекта фиксировалась ссылка на узел, в котором был найден заданный ключ (в случае успешного поиска), или ссылка на узел, после обработки которого поиск прекращается (в случае неуспешного поиска).

Псевдокод: P = tree Q = nil Whlie p <> nil do   q = p   if key = k(p) then     search = p     return   endif  if key < k(p) then     p = left(p)   else     p = right(p)   endif endwhile v = maketree(key, rec) if q = nil then   tree = v  else    if key < k(q) then     left(q) = v    else     right(q) = v   endif endif    search = v    return

Паскаль: p := tree; q := nil; whlie p <> nil do   begin     q := p;     if key = p^.k then       begin         search := p;         exit;       end;     if key < p^.k then       p := p^.left     else       p := p^.right;   end;            v := maketree(key, rec)  if q=nil then    tree:=v   else    if key < q^.k then     q^.left := v    else     q^.right := v;    search := v;

Полустатические структуры данных

К полустатическим структурам данных относят стеки, деки и очереди.

Списки

Это набор связанных элементов данных, которые в общем случае могут быть разного типа.

Пример списка:

E1, E2, ........, En,...   n > 1 и не зафиксировано.

Количество элементов списка может меняться в процессе выполнения программы. Различают 2 вида списков:

1) Несвязные

2) Связные

В несвязных списках связь между элементами данных выражена неявно. В связных списках в элемент данных заносится указатель связи с последующим или предыдущим элементом списка.

Стеки, деки и очереди - это несвязные списки. Кроме того они относятся к последовательным спискам, в которых неявная связь отображается их последовательностью. 

Последовательный поиск

Применяется в том случае, если неизвестна организация данных или данные неупорядочены. Тогда производится последовательный просмотр по всей таблице начиная от младшего адреса в оперативной памяти и кончая самым старшим.

Последовательный поиск в массиве (переменная search хранит номер найденного элемента).

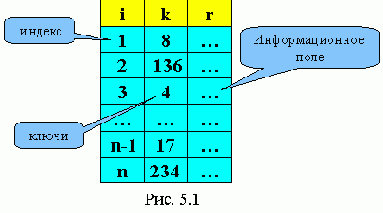
               for i:=1 to n

                 if k(i) = key then

                                        search = i

                                         return

                 endif

              next i

              search = 0

              return

На Паскале программа будет выглядеть следующим образом:

for i:=1 to n do

  if k[i] = key then

    begin

      search = i;

      exit;

    end;

search = 0;

exit;

Эффективность последовательного поиска в массиве можно определить как количество производимых сравнений М. Мmin = 1, Mmax = n. Если данные расположены равновероятно во всех ячейках массива, то Мср » (n + 1)/2.

Если элемент не найден в таблице и необходимо произвести вставку, то последние 2 оператора заменяются на

n = n + 1                                                  на Паскале

k(n) = key                                                n:=n+1;

r(n) = rec                                                 k[n]:=key;

search = n                                                r[n]:=rec;

return                                                       search:=n;

                                                                exit;

Если таблица данных задана в виде односвязного списка, то производится последовательный поиск в списке (рис. 5.2).

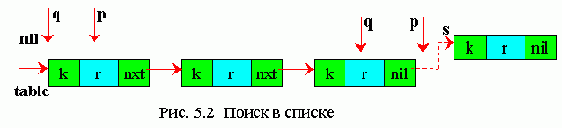
Варианты алгоритмов:

На псевдокоде: q=nil p=table while (p <> nil) do   if k(p) = key then     search = p     return   endif   q = p   p = nxt(p) endwhile s = getnode k(s) = key r(s) = rec nxt(s) = nil if q = nil then   table = s   else nxt(q) = s endif search = s return

На Паскале: q:=nil; p:=table; while (p <> nil) do   begin   if p^.k = key then     begin       search = p;       exit;     end;   q := p;   p := p^.nxt; end; New(s); s^.k:=key; s^.r:=rec; s.^nxt:= nil; if q = nil then table = s                else q.^nxt = s; search:= s; exit

Достоинством списковой структуры является ускоренный алгоритм удаления или вставки элемента в список, причем время вставки или удаления не зависит от количества элементов, а в массиве каждая вставка или удаление требуют передвижения примерно половины элементов. Эффективность поиска в списке примерно такая же, как и в массиве.

Эффективность последовательного поиска можно увеличить.

Пусть имеется возможность накапливать запросы за день, а ночью их обрабатывать. Когда запросы собраны, происходит их сортировка.

Постановка задачи

Осуществить исследование прямых методов сортировки:

- метод прямого  выбора;

- метод прямой  вставки;

- метод прямого обмена.

Исследование осуществить, используя массивы упорядоченных и неупорядоченных чисел по 10,100,1000 и 10000 элементов.

Представление деревьев

 

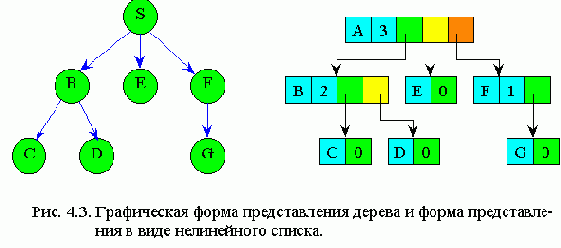
Наиболее удобно деревья представлять в памяти ЭВМ в виде связанных списков. Элемент списка должен содержать информационные поля, в которых содержится значение узла и степень исхода, а также - поля-указатели, число которых равно степени исхода (рис4.3). То есть, любой указатель элемента ориентирует данный элемент-узел с сыновьями этого узла.

ПРЕОБРАЗОВАНИЕ КЛЮЧЕЙ (РАССТАНОВКА)

Метод расстановок (хеширования) направлен на быстрое решение задачи о местоположении элемента в структуре данных. В методе расстановок данные организованы как обычный массив. Поэтому Н - отображение, преобразующее ключи в индексы массива, отсюда и появилось название «преобразование ключей», обычно даваемое этому методу. Следует заметить, что нет никакой нужды обращаться к каким-либо процедурам динамического размещения, ведь массив — это один из основных, статических объектов. Метод преобразования ключей часто используется для таких задач, где можно с успехом воспользоваться и деревьями.

Основная трудность, связанная с преобразованием ключей, заключается в том, что множество возможных значений значительно шире множества допустимых адресов памяти (индексов массива). Возьмем в качестве примера имена, включающие до 16 букв и представляющие собой ключи, идентифицирующие отдельные индивиды из множества в тысячу персон. Следовательно, мы имеем дело с 2616

возможными ключами, которые нужно отобразить в 103 возмож­ных индексов. Поэтому функция Н будет функцией класса «много значений в одно значение». Если дан некоторый ключ k, то первый шаг операции поиска — вычисление связанного с ним индекса h = H(k), а второй (совершенно необходимый) — проверка, действительно ли h идентифицирует в массиве (таблице) Т элемент с ключом k.

Тесты с ответами

Лабораторная работа 1. Полустатические структуры данных (стеки).

6.   В чём особенности очереди ?

-        открыта с обеих сторон (верный);

-        открыта с одной стороны на вставку и удаление;

-        доступен любой элемент.

7.   В чём сосбенности стека ?

-        открыт с обеих сторон на вставку и удаление;

-        доступен любой элемент;

-        открыт с одной стороны на вставку и удаление (верный).

8.   Какую дисциплину обслуживания принято называть FIFO ?

-        стек;

-        очередь (верный);

-        дек.

9.   Какая операция читает верхний элемент стека без удаления ?

-        pop;

-        push;

-        stackpop (верный).

10.         Каково правило выборки элемента из стека ?

-        первый элемент;

-        последний элемент (верный);

-        любой элемент.

Лабораторная работа 2.Списковые структуры данных (односвязные очереди).

6.   Как освободить память от удаленного из списка элемента ?

-        p=getnode;

-        ptr(p)=nil;

-        freenode(p) (верный);

-        p=lst.

7.   Как создать новый элемент списка с информационным полем D ?

-        p=getnode;

-        p=getnode; info(p)=D (верный);

-        p=getnode; ptr(D)=lst.

8.   Как создать пустой элемент с указателем p ?

-        p=getnode (верный);

-        info(p);

-        freenode(p);

-        ptr(p)=lst.

9.   Сколько указателей используется в односвязных списках ?

-        1 (верный);

-        2;

-        сколько угодно.

10.         В чём отличительная особенность динамических объектов ?

-        порождаются непосредственно перед выполнением программы;

-        возникают уже в процессе выполнения программы (верный);

-        задаются в процессе выполнения программы.

Лабораторная работа 3.Списковые структуры данных.

6.   При удалении элемента из кольцевого списка…

-        список разрывается;

-        в списке образуется дыра;

-        список становится короче на один элемент (верный).

7.   Для чего используется указатель в кольцевых списках ?

-        для ссылки на следующий элемент;

-        для запоминания номера сегмента расположения элемента;

-        для ссылки на предыдущий элемент (верный);

-        для расположения элемента в списке памяти.

8.   Чем отличается кольцевой список от линейного ?

-        в кольцевом списке последний элемент является одновременно и первым;

-        в кольцевом списке указатель последнего элемента пустой;



-        в кольцевых списках последнего элемента нет (верный);

-        в кольцевом списке указатель последнего элемента не пустой.

9.   Сколько указателей используется в односвязном кольцевом списке ?

-        1(верный);

-        2;

-        сколько угодно.

10.         В каких направлениях можно перемещаться в кольцевом двунаправленном списке ?

-        в обоих (верный);

-        влево;

-        вправо.

Лабораторная работа 4. Модель массового обслуживания.

6.   Чем отличается заявка первого приоритета от заявки второго приоритета ?

-        тем, что заявка второго приоритета обслуживается с вероятностью P=1, а заявка первого приоритета обслуживается с вероятностью P(B);

-        тем, что заявка второго приоритета становится в начало очереди, а первого приоритета становится в конец очереди (верный);

-        ничем, если есть очередь.

7.   Может ли заявка первого приоритета вытеснить из очереди заявку второго приоритета ?

-        да, если P(B)=1;

-        да;

-        нет (верный).

8.   Может ли на обслуживании находится заявка первого приоритета, если в очереди находится заявка второго приоритета ?

-        да, если P(B)=1;

-        да (верный);

-        нет.

9.   С помощью какой структуры данных наиболее рационально реализовать очередь ?

-        стек;



-        список (верный);

-        дек.

10.         Когда заявка покидает систему. Найдите ошибку.

-        если заявка обслужилась подложенное ей число тактов;

-        если заявка находится в очереди больше Т тактов;

-        если заявок второго приоритета стало больше, чем заявок первого приоритета (верный).

Лабораторная работа 5. Бинарные деревья (основные процедуры).

6.   Для включения новой вершины в дерево нужно найти узел, к которому её можно присоединить. Узел будет найден, если очередной ссылкой, определяющей ветвь дерева, в которой надо продолжать поиск, окажется ссылка:

-        p=right(p);

-        p=nil (верный);

-        p=left(p).

7.   Для написания процедуры над двумя деревьями необходимо описать элемент типа запись, который содержит поля:

-        Element=Запись

Left,Right : Указатели

Rec : Запись;

-        Element=Запись

Left : Указатель

Key : Ключ

Rec : Запись;

-        Element=Запись (верный)

Left, Right : Указатели

Кеу : Ключ

Rec : Запись.

8.   В памяти ЭВМ бинарное дерево удобно представлять в виде:

-        связанных линейных списков;

-        массивов;

-        связанных нелинейных списков (верный).

9.   Элемент t, на котрый нет ссылок:

-        корнем (верный);

-        промежуточным;

-        терминальным (лист).

10.         Дерево называется полным бинарным, если степень исходов вершин равна:



-        2 или 0 (верный);

-        2;

-        М или 0;

-        M.

Лабораторная работа 6. Сортировка методом прямого включения.

6.   Даны три условия окончания просеивания при сортировке прямым включением. Найдите среди них лишнее.

-        найден элемент a(i) с ключом, меньшим чем ключ у x;

-        найден элемент a(i) с ключом, большим чем ключ у x (верный);

-        достигнут левый конец готовой последовательности.

7.   Какой из критериев эффективности сортировки определяется формулой M=0,01*n*n+10*n ?

-        число сравнений (верный);

-        время, затраченное на написание программы;

-        количество перемещений;

-        время, затраченное на сортировку.

8.   Как называется сортировка, происходящая в оперативной памяти ?

-        сортировка таблицы адресов;

-        полная сортировка;

-        сортировка прямым включением;

-        внутренняя сортировка (верный);

-        внешняя сортировка.

9.   Как можно сократить затраты машинного времени при сортировке большого объёма данных ?

-        производить сортировку в таблице адресов ключей (верный);

-        производить сортировку на более мощном компьютере;

-        разбить данные на более мелкие порции и сортировать их.

10.         Существуют следующие методы сортировки.


Найдите ошибку.

-        строгие;

-        улудшенные;

-        динамические (верный).

Лабораторная работа 7. Сортировка методом прямого выбора.

6.   Метод сортировки называется устойчивым, если в процессе сортировки…

-        относительное расположенние элементов безразлично;

-        относительное расположение элементов с равными ключами не меняется (верный);

-        относительное расположение элементов с равными ключами изменяется;

-        относительное расположение элементов не определено.

7.   Улучшенные методы имеют значительное преимущество:

-        при большом количестве сортируемых элементов (верный);

-        когда массив обратно упорядочен;

-        при малых количествах сортируемых элементов;

-        во всех случаях.

8.   Что из перечисленных ниже понятий является одним из типов сортировки ?

-        внутренняя сортировка (верный);

-        сортировка по убыванию;

-        сортировка данных;

-        сортировка по возрастанию.

9.   Сколько сравнений требует улучшенный алгоритм сортировки ?

-        n*log(n) (верный);

-        en;

-        n*n/4.

10.         К какому методу относится сортировка, требующая n*n сравнений ключей ?

-        прямому (верный);

-        бинарному;



-        простейшему;

-        обратному.

Лабораторная работа 8. Сортировка с помощью прямого обмена.

6.   Сколько сравнений и пeрестановок элементов требуется в пузырьковой сортировке ?

-        n*lon(n);

-        (n*n)/4 (верный);

-        (n*n-n)/2.

7.   Сколько дополнительных переменных нужно в пузырьковой сортировке помимо массива, содержащего элементы ?

-        0 (не нужно);

-        всего 1 элемент (верный);

-        n переменных (ровно столько, сколько элементов в массиве).

8.   Как рассортировать массив быстрее, пользуясь пузырьковым методом ?

-        одинаково (верный);

-        по возрачстанию элементов;

-        по убыванию элементов.

9.   В чём заключается идея метода QuickSort ?

-        выбор 1,2,…n – го элемента для сравнения с остальными;

-        разделение ключей по отношению к выбранному (верный);

-        обмен местами между соседними элементами.

10.         Массив сортируется “пузырьковым” методом. За сколько проходов по массиву самый “лёгкий” элемент в массиве окажется вверху ?

-        за 1 проход (верный);

-        за n-1 проходов;

-        за n проходов, где n – число элементов массива.

Лабораторная работа 9. Сортировка с помощью дерева.

6.   При обходе дерева



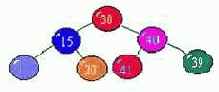
слева направо получаем последовательность…

-        отсортированную по убыванию;



-        неотсортированную (верный);

-        отсортированную по возрастанию.

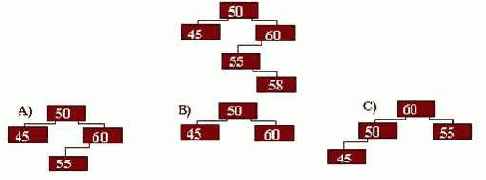
7.   Какое из трёх деревьев не является строго сбалансированным ?



-        A;

-        B(верный);

-        C.

8.   При обходе дерева слева направо его элемент заносится в массив…

-        при втором заходе в элемент (верный);

-        при первом заходе в элемент;

-        при третьем заходе в элемент.

9.   Элемент массива с ключом k=20 необходимо вставить в изображённое дерево так, чтобы дерево осталось отсортированным. Куда его нужно вставить ?



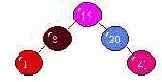
-        левым сыном элемента 30 (верный);

-        левым сыном элемента 41;

-        левым сыном элемента 8.

10.         При обходе какого дерева слева направо получается отсортированный по возрастанию массив ?



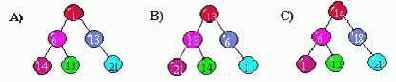
-        A;

-        B;

-        C (верный).

Лабораторная работа 10. Исследование методов линейного и бинарного поиска.

6.   Где эффективен линейный поиск ?

-        в списке;

-        в массиве;

-        в массиве и в списке (верный).

7.   Какой поиск эффективнее ?

-        линейный;

-        бинарный (верный);

-        без разницы.

8.   В чём суть бинарного поиска ?

-        нахожденние элемента массива x путём деления массива пополам каждый раз, пока элемент не найден (верный);



-        нахождение элемента x путём обхода массива;

-        нахождение элемента массива х путём деления массива.

9.   Как расположены элементы в массиве бинарного поиска ?

-        по возрастанию (верный);

-        хаотично;

-        по убыванию.

10.         В чём суть линейного поиска ?

-        производится последовательный просмотр от начала до конца и обратно через 2 элемента;

-        производится последовательный просмотр элементов от середины таблицы;

-        производится последовательный просмотр каждого элемента (верный).

Лабораторная работа 11. Исследование методов поиска с перемещением в начало и транспозицией.

6.   Где наиболее эффективен метод транспозиций ?

-        в массивах и в списках (верный);

-        только в массивах;

-        только в списках.

7.   В чём суть метода перестановки ?

-        найденный элемент помещается в голову списка (верный);

-        найденный элемент помещается в конец списка;

-        найденный элемент меняется местами с последующим.

8.   В чём суть метода транспозиции ?

-        перестановка местами соседних элементов;

-        нахождение одинаковых элементов;

-        перестановка найденного элемента на одну позицию в сторону начала списка (верный).

9.   Что такое уникальный ключ ?

-        если разность значений двух данных равна ключу;



-        если сумма значений двух данных равна ключу;

-        если  в таблице есть только одно данное с таким ключом (верный).

10.         В чём состоит назначение поиска ?

-        среди массива данных найти те данные, которые соответствуют заданному аргументу (верный);

-        определить, что данных  в массиве нет;

-        с помощью данных найти аргумент.

Лабораторная работа 12. Поиск по дереву с включением.

6.   В каком дереве при бинарном поике нужно перебрать в среднем N/2 элементов ?



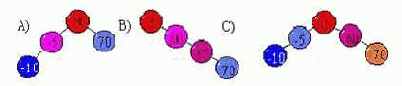
-        A;

-        B (верный);

-        C.

7.   Сколько нужно перебрать элементов в сбалансированном дереве ?

E) N/2;

F)  Ln(N);

G)            Log2(N);

H)            eN.

-        A;

-        B;

-        C (верный);

-        D.

8.   Выберете вариант дерева, полученного после вставки узла  -1.



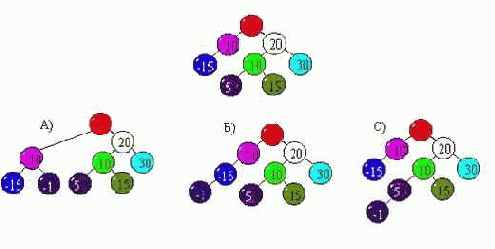
-        A (верный);

-        B;

-        C.

9.   К какому элементу присоединить элемент 40 для вставки его в данное дерево ?



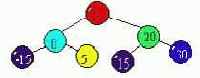
-        к 30-му (верный);

-        к 15-му;

-        к –15-му;

-        к 5-му.

10.         Какой вид примет дерево после встаки элемента с ключом 58 ?





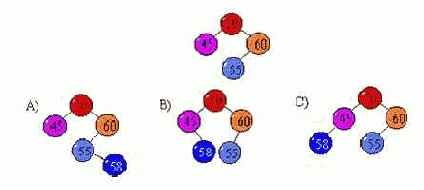
-        A (верный);

-        B;

-        C.

Лабораторная работа 13. Поиск по дереву с исключением.

6.   Выберете вариант дерева, полученного после удаления узла –3.



-        A;

-        B (верный);

-        C.

7.   Какой вариант дерева получится после удаления элемента –1, а затем –8 ?



-        A;

-        B (верный);

-        C.

8.   Выберете вариант дерева, полученного после удаления узла с индексом 0.



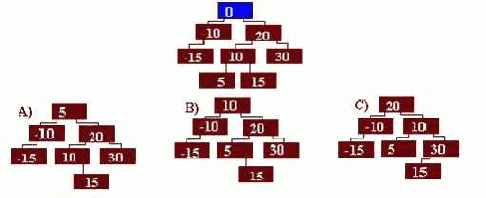
-        A (верный);

-        B;

-        C.

9.   Какие из следующих пар чисел могут стать корнями дерева после удаления элемента 10 в соответсвии с двумя способами удаления узла, имеющего двух сыновей ?



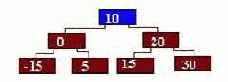
-        0 или 15;

-        0 или 20;

-        5 или 30;

-        5 или 15 (верный).

10.         Какой вид примет дерево после удаления элемента с ключом 58 ?



-        A (верный);

-        B;

-        C.

 





 

 

Лойко  Валерий  Иванович

 

 

Структуры и алгоритмы

обработки данных

 

Учебное пособие для вузов

Авторская правка

ЛР № 02334 от 14.07.2004

Подписано в печать  2.11.2000                          Формат 60 х 84

Бумага Типографская                                         Офсетная печать

Печ. л.  13,5                                                         Заказ № 618

Тираж 500

350044, Краснодар,  Калинина, 13

Отпечатано в типографии КубГАУ

Примерный перечень курсовых работ

   1) Исследование стеков.

   2) Исследование очередей.

   3) Исследование кольцевых структур.

   4) Исследование полустатических структур.

   5) Исследование линейных одно- и двусвязных списков.

   6) Исследование деревьев бинарного поиска.

   7) Исследование методов сортировки включением.

   8) Исследование методов сортировки выбором.

   9) Исследование методов сортировки обменом.

 10) Исследование методов сортировки с помощью деревьев.

 11) Исследование улучшенных методов сортировки.

 12) Исследование линейного, индексного и бинарного поисков.

 13) Исследование методов оптимизации поиска.

 14) Исследование задач поиска по дереву.

Примеры типичных операций над списками

Задача 1.

Требуется просмотреть список и удалить элементы, у которых информационные поля равны 4.

Обозначим P - рабочий указатель, в начале процедуры P = Lst. Введем также указатель Q, который отстает на один элемент от P. Когда указатель P найдет элемент, последний будет удален относительно указателя Q как последующий элемент.

Q = Nil

P = Lst

While P <> Nil do

  If Info(P) = 4 then

    If Q = Nil then

      Pop(Lst)

      FreeNode(P)

      P = Lst

    Else

      DelAfter(Q, X)

    EndIf

  Else

    Q = P

    P = Ptr(P)

  EndIf

EndWhile

Задача 2.

Дан упорядоченный по возрастанию Info - полей список. Необходимо вставить в этот список элемент со значением X, не нарушив упорядоченности списка.

Пусть X = 16. Начальное условие: Q = Nil, P = Lst. Вставка элемента должна произойти между 3 и 4 элементом (рис.3.10).

Q =Nil

P = Lst

While (P <> Nil) and (X > Info(P)) do

  Q = P

  P = Ptr(P)

EndWhile

if Q = Nil then

  Push(Lst, X)

EndIf

InsAfter(Q, X)

Реализация примеров на языке Паскаль:

Задача 1:

Q:=nil;

P:=Lst;

While P <> nil do

  If P^.Info = 4 then

    begin   

      If Q = nil then

        begin

          Pop(Lst);

          P:=Lst;

        end

      Else Delafter(Q,X);

    End;

  Else

    begin

      Q:=P;

      P:=P^.Next;

    end;

  end;

Задача 2:

Q:=nil;

P:=Lst;

While (P <> nil) and (X > P^.Info) do

  begin

    Q:=P;

    P:=P^.Next;

  end;

{В эту точку производится вставка}

If Q = nil then Push(Lst, X);

InsAfter(Q, X);

End;

Процедура поиска по бинарному дереву

Назначение этой процедуры в том, чтобы по заданному ключу осуществить поиск узла дерева. Длительность операции поиска (число узлов, которое надо перебрать для этой цели) зависит от структуры дерева. Действительно, дерево может быть вырождено в однонаправленный список (иметь единственную ветвь) - такое дерево может возникнуть, если элементы поступали в дерево в порядке возрастания (убывания) их ключей, например :

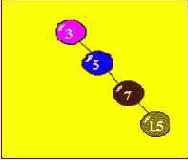
В этом случае время поиска будет такое же, как и в однонаправленном списке, т.е. в среднем придется перебрать N/2 элементов.

Наибольший эффект использования дерева достигается в том случае, когда дерево "сбалансировано". В этом случае для поиска придется перебрать не более LOG2N элементов.

Опишем процедуру поиска. Переменной search будет присваиваться указатель на найденное звено :

p=tree

    WHILE p<>nil DO

         IF key=k (p)

            THEN search=p

           RETURN

         END IF

         IF key<>k (p)

            THEN p=left (p)

            ELSE p=right (p)

         END IF

     END WHILE

     search=nil

     RETURN

Процедура прибавления элемента в начало списка.

      p = getnode           Node(p) - элемент, на который указывает

      info(p) = d                             указатель Р

      ptr(p) = lst             info(ptr(p)) - информационное поле следующего

      lst = b                           элемента списка

Процедура прибавления элемента в список.

      p = getnode         q - вставляемый

      info(p) = x

      ptr(q) = ptr(p)

      ptr(p) = q

Процедура создания бинарного дерева

Для построения дерева необходимо создать в памяти ЭВМ элемент следующего типа:

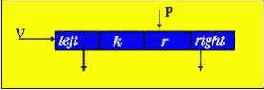
P, Q - рабочие указатели

V=maketree(key,rec) - процедура, которая создает сегмент ключа и записи

P=getnode - генерация нового элемента

r=rec

k=key

V=P

left=nil

right=nil

tree - указатель на корень дерева

Введем сначала первое значение ключа, потом сгенерируем сам элемент узла дерева процедурой maketree. Далее идем по циклу до тех пор, пока указатель не передвинется на нулевое значение.

READ(key,rec)

tree=maketree(key,rec)

WHILE not eof DO

  READ(key,rec)

  V=maketree(key,rec)

  WHILE P<>nil DO

     Q=P

     IF key=k(P)

       THEN P=left(P)

       ELSE P=right(P)

    END IF

 END WHILE

 IF P=nil

  THEN WRITELN(' Это корень');

  tree=V

  ELSE IF key<k(q)

           THEN left(P)=V

           ELSE right(P)=V

          END IF

   END IF

END WHILE

Процедура удаления из начала списка.

      p = lst

      х = info(p)

      lst =   ptr(p)

      freenode(p)   -  делает свободный узел с указателем

Процедура удаления из списка

      q = ptr(p)          q - удаляемый

      ptr(p) = ptr(q)

      x = info(p)

      freenode(q)

Процедура удаления элемента из бинарного дерева

Удаление узла не должно нарушать упорядоченность дерева. При удалении элемента из бинарного дерева с заданным ключом различают три случая :

1) удаляемый узел является листом, в этом случае он просто удаляется, не нарушая этим упорядоченность дерева ;

2) если удаляемый узел имеет только одного сына, то сын перемещается на место удаляемого отца ;

4) если у удаляемого узла 2 сына. В этом случае на место удаляемого отца помещается либо его предшественник в симметричном обходе (обход слева направо), либо его последователь.

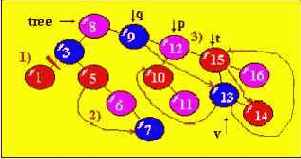
Разработаем алгоритм для 3-его случая (вершина-узел имеет 2-х сыновей), вместо удаляемого узла поставим его приемника в симметричном обходе. Предшественником удаляемого узла 12 является самый правый узел левого поддерева - узел 11, а приемником или последователем при симметричном обходе (обход слева направо) является самый левый узел правого поддерева - узел 13.

Будем использовать следующие указатели :

p - рабочий указатель;

q - отстает на один шаг от p;

v - указывает приемника;

t - отстает от v на один шаг;

s - опережает v на один шаг.

1) Процедурой поиска элемента находим удаляемый элемент. Указатель p указывает на удаляемый элемент.

2) Установим указатель v на узел, который будет замещать удаляемый элемент.

      IF left (p)=nil

        THEN v=right (p)

        ELSE IF right (p)=nil

                   THEN v=left (p)

                   ELSE t=p

                            v=right (p)

                            s=left (v)

WHILE s<>nil

            t=v

            v=s

            s=left (v)

END WHILE

      IF t<>p

        THEN WRITE (v не является сыном p)

                  left (t)=right (v)

                 right (v)=right (p)

      END IF

left (v)=left (p)

       IF q=nil

         THEN WRITE (v корень)

                   tree=v

         RETURN

       END IF

       IF p=left (q)

         THEN left (q)=v

         ELSE right (q)=v

       END IF

    END IF

END IF

FREENODE (p) (процедура создает свободный узел, т.е. очищает ячейку памяти, в которой находится удаленный элемент)

RETURN

Процедура включения элемента в дерево

Для включения новой записи в дерево прежде всего нужно найти тот его узел, к которому можно "подвесить" (присоединить) новый элемент. Алгоритм поиска нужного узла тот же самый, что и при поиске узла с заданным ключом. Этот узел будет найден в тот момент, когда в качестве очередной ссылки, определяющей ветвь дерева, в которой надо продолжить поиск, окажется ссылка NIL.

Однако непосредственно использовать описанную выше процедуру поиска нельзя, потому что по окончании вычисления ее значения не фиксируется тот узел, из которого была выбрана ссылка NIL.

Модифицируем описание процедуры поиска так, чтобы в качестве ее побочного эффекта фиксировалась ссылка на узел, в котором был найден заданный ключ (в случае успешного поиска), или ссылка на узел, после обработки которого поиск прекращен (в случае неуспешного поиска). И опишем процедуру включения элемента в дерево, учитывая, что в дереве нет узла с тем же ключом, что и у включаемого элемента.

q=nil

p=tree

WHILE p<>nil DO

            q=p

      IF key=k (p)

        THEN search=p

        RETURN

      END IF

      IF key<k (p)

        THEN p=left (p)

        ELSE p=right (p)

      END IF

END WHILE

{Узел с заданным ключом не найден, требуется вставка элемента. На узел предполагаемого отца указывает q.}

V=maketree (key, rec)

{Нужно выяснить, левым или правым сыном будет вставляемый элемент V.}

 IF key<k (q)

   THEN left (q)=V

   ELSE right (q)=V

 END IF

 search=V

RETURN

Процедуры "обхода" дерева

Пусть задано бинарное дерево :

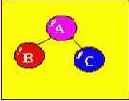
Существуют три принципа обхода бинарных деревьев. Рассмотрим их на примере заданного дерева :

1) Обход сверху вниз (корень посещается ранее, чем поддеревья) : A, B, C ;

2) Слева направо : B, A, C ;

3) Снизу вверх (корень посещается после поддеревьев) : B, C, A .

Наиболее часто применяется 2-ой способ, узлы посещаются в порядке возрастания значения их ключа.

Рекурсивные процедуры обхода дерева :

1) PROCEDURE pretrave (tree)

         IF tree<>nil

           THEN PRINT info (tree)

                     pretrave (left (tree))

                     pretrave (right (tree))

         END IF

      RETURN

2) PROCEDURE intrave (tree)

         IF tree<>nil

           THEN intrave (left (tree))

                      PRINT info (tree)

                      intrave (right (tree))

         END IF

         RETURN

3) PROCEDURE postrave (tree)

         IF tree<>nil

           THEN postrave (left (tree))

                      postrave (right (tree))

                      PRINT info (tree)

         END IF

         RETURN

Прохождение бинарных деревьев

В зависимости от  последовательности обхода поддеревьев различают три вида обхода (прохождения) деревьев (рис.4.9):

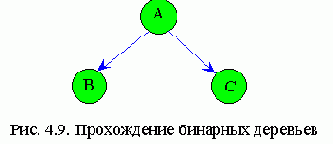
1. Сверху вниз А, В, С.

2. Слева направо или симметричное прохождение В, А, С.

3. Снизу вверх В, С, А.

Наиболее часто применяется второй способ.

Ниже приведены рекурсивные алгоритмы прохождения бинарных деревьев.

subroutine pretrave (tree) ‘сверху вниз if tree <> nil then   print info(tree)   pretrave(left(tree))   pretrave(right(tree)) endif return subroutine intrave (tree) ‘симметричный if tree <> nil then   intrave(left(tree))   print info(tree)   intrave(right(tree)) endif return

Procedure pretrave (tree: tnode) Begin   if tree <> nil then     begin       WriteLn(Tree^.Info);       Pretrave(Tree^.left);       Pretrave(Tree^.right);      End; end; procedure intrave (tree: tnode) begin   if tree <> nil then     begin       intrave(Tree^.left);       writeLn(Tree^.info);        intrave(Tree^.right);      end; end;

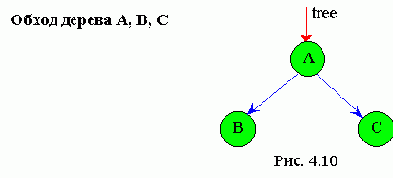
Поясним подробнее рекурсию алгоритма обхода дерева слева направо.

Пронумеруем строки алгоритма

intrave (tree):

 

1                   if tree <> nil

2                      then intrave (left(tree))

3                            print info (tree)

4                           intrave (right (tree))

5                      endif

6                   return

Обозначим указатели: t > tree;  l >

left;  r > right

На приведенном рис. 4.11 проиллюстрирована последовательность вызова процедуры intrave (tree) по мере обхода узлов простейшего дерева, изображенного на рис. 4. 10.

Реализация стеков с помощью односвязных списков 

Любой односвязный список может рассматриваться в виде стека. Однако список по сравнению со стеком в виде одномерного массива имеет преимущество, так как заранее не задан его размер.

Стековые операции, применимые к спискам

1). Чтобы добавить элемент в стек, надо в алгоритме заменить указатель Lst на указатель Stack (операция Push(S, X)).

P = GetNode

Info(P) = X

Ptr(P) = Stack

Stack = P

2) Проверка стека на пустоту (Empty(S))

If Stack = Nil then Print “Стек пуст”

Stop

3) Выборка элемента из стека (POP(S))

P = Stack

X = Info(P)

Stack = Ptr(P)

FreeNode(P)

Реализация на Паскале:

Стек

Вместо указателя Lst используется указатель Stack

Процедура Push (S, X)

procedure Push(var Stack: PNode; X: Integer);

var

  P: PNode;

begin

  New(P);

  P^.Info:=X;

  P^.Next:=Stack;

  Stack:=P;

end;

Проверка на пустоту (Empty)

function Empty(Stack: PNode): Boolean;

begin

  If Stack = nil then Empty:=True Else Empty:=False;

end;

Процедура Pop

procedure Pop(var X: Integer; var Stack: PNode);

var

  P: PNode;

begin

  P:=Stack;

  X:=P^.Info;

  Stack:=P^.Next;

  Dispose(P);

end;

Операции с очередью, применимые к спискам.

Указатель начала списка принимаем за указатель начала очереди F, а указатель R, указывающий на последний элемент списка - за указатель конца очереди.

1) Операция удаления из очереди (Remove(Q, X)).

Операция удаления из очереди должна проходить из ее начала.

P = F

F = Ptr(P)

X = Info(P)

FreeNode(P)

2) Проверка очереди на пустоту. (Empty(Q))

If F = Nil then Print “Очередь пуста”

Stop

3) Операция вставки в очередь. (Insert(Q, X))

Операция вставки в очередь должна осуществляться к ее концу.

P = GetNode

Info(P) = X

Ptr(P) = Nil

Ptr(R)= P

R = P

Реализация на Паскале:

procedure Remove(var X: Integer; Fr: PNode);

var

  P: PNode;

begin

  New(P);     

  P:=Fr;

  X:=P^.Info;

  Fr:=P^.Next; 

  Dispose(P);

end;

function Empty(Fr: PNode): Boolean;

begin

  If Fr = nil then Empty:=True Else Empty:=False;

end;

procedure Insert(X: Insert; var Re: PNode);

var

  P: PNode;

begin

  New(P);

  P^.Info:=X;

  P^.Next:=nil;

  Re^.Next:=P;

end;

Рекурсивные структуры данных

Рассмотрим рекурсивные алгоритмы и рекурсивные структуры данных.

Рекурсия - процесс, протекание которого связано с обращением к самому себе (к этому же процессу).

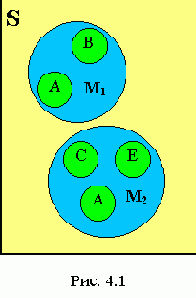
Пример рекурсивной структуры данных - структура данных,  элементы которой являются такими же структурами данных (рис. 4.1).

Результаты исследования

 

Сортировка 10 элементов:
- упорядоченных по возрастанию
метод		прямого выбора		прямой вставки		прямого обмена
сравнений		45		45		45
перемещений		11		33		33
- неупорядоченных (случайных)
метод		прямого выбора		прямой вставки		прямого обмена
сравнений		45		45		45
перемещений		27		27		27
- упорядоченных по убыванию
метод		прямого выбора		прямой вставки		прямого обмена
сравнений		45		45		45
перемещений		0		0		0
Сортировка 100 элементов:
- упорядоченных по возрастанию
метод		прямого выбора		прямой вставки		прямого обмена
сравнений		4950		4950		4950
перемещений		2643		4862		4862
- неупорядоченных (случайных)
метод		прямого выбора		прямой вставки		прямого обмена
сравнений		4950		4950		4950
перемещений		2558		2558		2558
- упорядоченных по убыванию
метод		прямого выбора		прямой вставки		прямого обмена
сравнений		4950		4950		4950
перемещений		0		0		0
Сортировка 1000 элементов:
- упорядоченных по возрастанию
метод		прямого выбора		прямой вставки		прямого обмена
сравнений		499500		499500		499500
перемещений		241901		498442		498442
-  неупорядоченных (случайных)
метод		прямого выбора		прямой вставки		прямого обмена
сравнений		499500		499500		499500
перемещений		244009		250366		250366
- упорядоченных по убыванию
метод		прямого выбора		прямой вставки		прямого обмена
сравнений		499500		499500		499500
перемещений		0		0		0
Сортировка 10000 элементов:
- упорядоченных по возрастанию
метод		прямого выбора		прямой вставки		прямого обмена
сравнений		49995000		49995000		49995000
перемещений		25003189		49984768		49984768
-  неупорядоченных (случайных)
метод		прямого выбора		прямой вставки		прямого обмена
сравнений		49995000		49995000		49995000
перемещений		18392665		24986578		24986578
- упорядоченных по убыванию
метод		прямого выбора		прямой ставки		прямого обмена
сравнений		49995000		49995000		49995000
перемещений		0		0		0

Символьный тип - CHAR

Тип CHAR содержит 26 прописных латинских букв и 26 строчных, 10 арабских цифр и некоторое число других графических символов, например, знаки пунктуации.

Подмножества букв и цифр упорядочены и "соприкасаются", т.е.

       ("A"<= x)&(x <= "Z") - x представляет собой прописную букву

       ("0"<= x)&(x <= "9") -  x представляет собой цифру

Тип CHAR содержит некоторый непечатаемый символ, пробел, его можно

использовать как разделитель.

 Операции:

a) Присваивания

b) Сравнения

c) Определения номера данной литеры в системе кодирования. ORD(Wi)

d) Нахождение литеры по номеру. CHR(i)

e) Вызов следующей литеры. SUCC(Wi)

f) Вызов предыдущей литеры. PRED(Wi)

Сортировка

При обработке данных важно знать  информационное поле данных и размещение их в машине.

Различают внутреннюю и внешнюю сортировку:

- внутренняя сортировка - сортировка в оперативной памяти;

- внешняя сортировка - сортировка во внешней памяти.

Сортировка - это расположение данных в памяти в регулярном виде по их ключам. Регулярность рассматривают как возрастание (убывание) значения ключа от начала к концу в массиве.

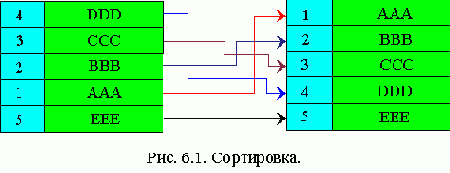
Если сортируемые записи занимают большой объем памяти, то их перемещение требует больших затрат. Для того, чтобы их уменьшить, сортировку производят в таблице адресов ключей, делают перестановку указателей, т.е. сам массив не перемещается. Это метод сортировки таблицы адресов.

При сортировке могут встретиться одинаковые ключи. В этом случае при сортировке желательно расположить после сортировки одинаковые ключи в том же порядке, что и в исходном файле. Это - устойчивая сортировка.

Эффективность сортировки можно рассматривать с нескольких критериев:

-   время, затрачиваемое на сортировку;

-   объем оперативной памяти, требуемой для сортировки;

-   время, затраченное программистом на написание программы.

Выделяем первый критерий, поскольку будем рассматривать только методы сортировки «на том же месте», то есть не резервируя для процесса сортировки дополнительную память. Эквивалентом затраченного на сортировку времени можно считать количество сравнений при выполнении сортировки и количество перемещений.

Порядок числа сравнения при сортировке лежит в пределах от  О (n log n)   до О (n2);    О (n) - идеальный  и недостижимый случай.

Различают следующие методы сортировки:

-   строгие (прямые) методы;

-   улучшенные методы.

Строгие методы:

1)                 метод прямого включения;

2)                 метод прямого выбора;

3)                 метод прямого обмена.

Эффективность этих трех методов примерно одинакова.

Сортировка методом прямого включения

Такой метод  широко используется при игре в карты. Элементы мысленно делятся на уже готовую последовательность  a1,...,ai-1 и исходную последовательность. При каждом шаге, начиная с i = 2  и увеличивая i  каждый раз на единицу, из исхожной последовательности извлекается i-й элемент и перекладывается  в готовую последовательность, при этом он вставляется на нужное место.На рис. 6.2 показан в качестве примера процесс сортировки  с помощью включения шести случайно выбранных чисел. Алгоритм этой сортировки таков:

for i = 2 to n

  x = a(i)

  находим место среди а(1)…а(i) для включения х

next i

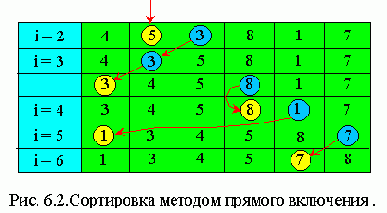
Для сортировки методом прямого включения пользуются следующими приемами:

Псевдокод: Без барьера: for i = 2 to n     x = a(i)     for j = i - 1 downto 1       if x < a(j )          then  a( j + 1) = a(j )          else  go to  L                      endif      next j  L:  a( j + 1) = x  next i  return    С барьером: for i = 2 to n    x = a(i)    a(0) = x {a(0) - барьер}    j = i - 1    while  x < a(j )  do      a( j +1) = a(j )      j = j - 1    endwhile     a( j +1) = x next i return

Паскаль: Без  барьера: for i:= 2 to n do   begin     x:= a(i);     for j:= i - 1downto 1 do       if x < a(j ) then          a(j +1):= a(j )        else  goto  1;       end;      end; 1:   a(j + 1):= x;   end;   end; С барьером:   for i := 2 to n do     begin       x:= a(i);       a(0):= x; {a(0) - барьер}       j:= i - 1;       while  x < a(j ) do         begin           a(j +1):= a(j );            j:=j - 1;        end;        a(j +1):= x;   end;

Эффективность алгоритма

 

Число сравнений ключей Ci при i- м просеивании самое большее равно i-1, самое меньшее - 1; если предположить, что все перестановки из N ключей равновероятны, то среднее число сравнений = i/2. Число же пересылок Mi=Ci+3 (включая барьер). Минимальные оценки встречаются в случае уже упорядоченной исходной последовательности элементов, наихудшие же оценки - когда они первоначально расположены в обратном порядке. В некотором смысле сортировка с помощью включения демонстрирует истинно естественное поведение. Ясно, что приведенный алгоритм описывает процесс устойчивой сортировки: порядок элементов с равными ключами при нем остается неизменным.

Количество сравнений в худшем случае, когда массив отсортирован противоположным образом, Сmax = n(n - 1)/2, т. е. - О (n2).   Количество перестановок Mmax = Cmax + 3(n-1), т.е.  -  О (n2). Если же массив уже отсортирован, то число сравнений и перестановок минимально: Cmin  = n-1; Mmin = =3(n-1).

Сортировка методом прямого выбора

Этот прием основан на следующих принципах:

1. Выбирается элемент с наименьшим ключом.

2. Он меняется местами с первым элементом a 1.

3. Затем этот процесс повторяется с оставшимися n-1 элементами, n-2 элементами и т.д. до тех пор, пока не останется один, самый "большой" элемент.

Алгоритм формулируется так:

for i = 1 to n - 1   x = a(i)   k = i   for j = i + 1 to n     if  a(j) < x  then       k = j       x = a(k)     endif   next j   a(k) = a(i)   a(i) = x next i return

for i := 1 to n - 1 do   begin     x := a[i];     k := i;     for j := i + 1 to n do       if a[j] < x then         begin           k := j;           x := a[k];         end;     a[k] := a[i];     a[i] := x;   end;

 

Эффективность алгоритма:

Число сравнений ключей C, очевидно, не зависит от начального порядка ключей. Можно сказать, что в этом смысле поведение этого метода менее естественно, чем поведение прямого включения. Для C  при любом расположении ключей имеем:

C = n(n-1)/2

Порядок числа сравнений, таким образом, О(n2)

Число перестановок  минимально Мmin = 3(n - 1) в случае изначально упорядоченных ключей и максимально, Мmax = 3(n - 1) + С, т.е. порядок О(n2), если первоначально ключи располагались в обратном порядке.

В худшем случае сортировка прямым выбором дает порядок n2, как  для   числа сравнений, так и для числа перемещений.

 

Сортировка с помощью прямого обмена (пузырьковая сортировка)

Классификация методов сортировки редко бывает осмысленной. Оба разбиравшихся до этого метода можно тоже рассматривать как "обменные" сортировки. В данном же, однако, разделе  описан метод, где обмен местами двух элементов представляет собой характернейшую особенность процесса. Изложенный ниже алгоритм прямого обмена основывается на сравнении и смене мест для пары соседних элементов и продолжении этого процесса до тех пор, пока не будут упорядочены все элементы.

Как и в упоминавшемся методе прямого выбора, мы повторяем проходы по массиву, сдвигая каждый раз наименьший элемент оставшейся последовательности к левому концу массива. Если мы будем рассматривать массивы как вертикальные, а не горизонтальные построения, то элементы можно интерпретировать как пузырьки в чане с водой, причем вес каждого соответствует его ключу. В этом случае при каждом проходе один пузырек как бы поднимается до уровня, соответствующего его весу (см. рис.6.3).

Такой метод широко известен под именем "пузырьковая сортировка". В своем простейшем виде он представлен ниже.

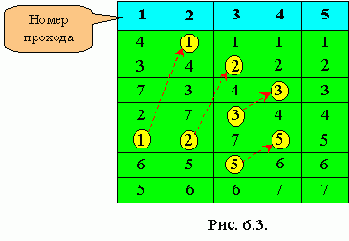
Программы на псевдокоде и Паскале:

for i = 2 to n   for j = n to i step -1     if a(j) < a(j - 1) then       x = a(j - 1)       a(j - 1) = a(j)       a(j) = x     endif    next j next i return

for i := 2 to n do   for j := n downto i do     if a[j] < a[j - 1]then       begin         x := a[j - 1];         a[j - 1] := a[j];         a[j] := x;       end;   end; end;

В нашем случае получился один проход “вхолостую”. Чтобы лишний раз не переставлять элементы, можно ввести флажок fl, который остается в значении false , если при очередном проходе не будет произведено ни одного обмена. На нижеприведенном алгоритме добавления отмечены курсивом.

fl = true

for i = 2 to n

if fl = false then return

endif

fl = false

  for j = n to i step -1

    if a(j) < a(j - 1) then

         fl = true

      x = a(j - 1)

      a(j - 1) = a(j)

      a(j) = x

    endif

           next j

next i

return

Улучшением пузырькового метода является шейкерная сортировка, где после каждого прохода меняют направление во внутреннем цикле.

Эффективность алгоритма:

Число сравнений Cmax = n(n-1)/2   ,               О(n2).

Число перемещений Мmax=3Cmax=3n(n-1)/2,   О(n2).

Если массив уже отсортирован и применяется алгоритм с флажком, то достаточно всего одного прохода, и тогда получаем минимальное число сравнений

Cmin = n - 1,                      О(n),

а перемещения вообще отсутствуют

Сравнительный анализ прямых сортировок показывает, что обменная "сортировка"  в классическом виде представляет собой нечто среднее между сортировками с помощью включений и с помощью выбора. Если же в нее внесены приведенные выше усовершенствования, то для достаточно  упорядоченных массивов пузырьковая сортировка даже имеет преимущество.

Сортировка Шелла (сортировка с уменьшающимся шагом)

В 1959 году Д. Шеллом было предложено усовершенствование сортировки с помощью метода прямого включения. Работа его представлена на рис. 6.5:

Сначала отдельно группируются и сортируются элементы, отстоящие друг от друга на расстоянии 4. Такой процесс называется четверной сортировкой. После первого прохода элементы перегруппировываются - теперь каждый элемент группы отстоит от другого на 2 позиции - и вновь сортируются. Это называется двойной сортировкой. И, наконец, на третьем проходе идет обычная или одиночная сортировка.

На первый взгляд можно засомневаться: если необходимо несколько процессов сортировки, причем в каждый включаются все элементы, то не добавят ли они больше работы, чем сэкономят? Однако, на каждом этапе либо сортируется относительно мало элементов, либо элементы уже довольно хорошо упорядочены и требуют сравнительно немного перестановок.

Ясно, что такой метод в результате дает упорядоченный массив, и, конечно, сразу же видно, что каждый проход от предыдущих только выигрывает; также очевидно, что расстояния в группах можно уменьшать по разному, лишь бы последнее было единичным, ведь в самом плохом случае последний проход и сделает всю работу.

Приводимый алгоритм основан на методе прямой вставки без барьера и не ориентирована на некую определенную последовательность расстояний, хотя в нем для конкретности заданы шаги 5, 3 и 1.

При использовании метода барьера  каждая из сортировок нуждается в постановке своего собственного барьера, и программу для определения его местонахождения необходимо делать насколько возможно простой. Поэтому приходится расширять массив до [-h1..N].

h[1..t] - массив размеров  шагов

a[1..n] - сортируемый массив

k - шаг сортировки

x - значение вставляемого элемента

Subroutine  ShellSort   Псевдокод: const t = 3           h(1) = 5           h(2) = 3           h(3) = 1   for m = 1 to t     k = h(m)     for i = k + 1 to n       x = a(i)       for j = i - k to 1 step -k         if  x < a(j) then           a( j+k) = a(j)         else            goto L          endif        next j   L:  a(j+k) = x       next i      next m     return

Паскаль: const   t = 3;             h(1) = 5;             h(2) = 3;             h(3) = 1; var   h: array [1..t] of integer;   a: array [1..n] of integer;    k, x, m, t, i, j: integer;  begin    for  m = 1 to t do      begin        k:= h(m);        for i = k + 1 to n do          begin           x:= a(i);                      for j = i-k  downto k   do              begin               if  x < a(j ) then                 a(j+k):= a(j);                else                  goto 1;               end ;              end;             end; 1:          a(j+1) = x ;          end;        end .

<
Не доказано, какие расстояния дают наилучший результат, но они не должны быть множителями один другого.

Д. Кнут предлагает такую последовательность шагов (в обратном порядке): 1, 3, 7, 15, 31, … То есть:  h m-1 = h m + 1,

t = log2n - 1. При такой организации алгоритма его эффективность имеет порядок O ( n1.2)

Контрольные вопросы

        1.        Что такое сортировка?

        2.        Назовите основные методы сортировки.

        3.        Какие методы сортировки относятся к строгим?

        4.        Какие методы сортировки относятся к улучшенным?

        5.        Какая сортировка называется устойчивой?

        6.        В чем состоит суть метода прямого включения?

        7.        В чем состоит суть метода прямого выбора?

        8.        В чем состоит суть метода прямого обмена?

        9.        Назовите разницу между этими тремя методами.

     10.     Какой метод сортировки является самым эффективным?

     11.     К какому из основных методов относится метод Шелла?

Создание дерева бинарного поиска :

(псевдокод)

  writeln(' Введите элемент массива ');

  readln(key);

  tree:=maketree(key);

  p:=tree;

  while not eof do

    begin

      readln(key);

      v:=maketree(key);

      while p<>nil do

         begin

             q:=p;

             if key<k(p) then p:=left(p)

             else p:=right(p);

         end;

         if p=nil then

            begin

                writeln('Это корень');

                tree:=v;

            end

            else

               if key<k(q) then left(p):=v

               else right(p):=v;

    end;

При обходе дерева слева - направо получаем отсортированный массив 20, 30, 35, 45, 60, 70, 82, 85, 86, 87, 88, 90. Элемент дерева заносится в массив при втором заходе в него (на рисунке вторые заходы показаны зелеными стрелками).

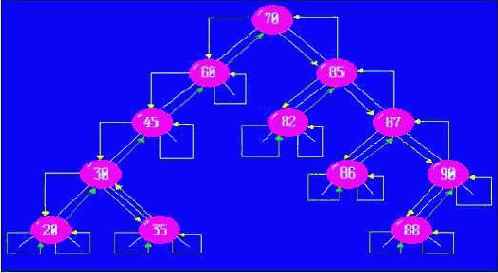
Статические и полустатические структуры данных

Структуры данных - это совокупность элементов данных и отношений между ними. При этом под элементами данных может подразумеваться как простое данное так и структура данных. Под отношениями между данными понимают функциональные связи между ними и указатели на то, где находятся эти данные.

Графическое представление элемента структуры данных.

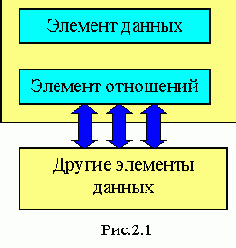
Элемент отношений - это совокупность всех связей элемента с другими элементами данных, рассматриваемой структуры.

S:=(D,R)

Где S - структура данных, D - данные и R - отношения.

Как бы сложна ни была структура данных, в конечном итоге она состоит из простых данных (см. рис. 2.2, 2.3).

 

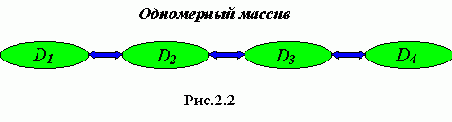
Стеки

Очередь вида LIFO (Last In First Out - Последним пришел, первым ушел ), при которой на обслуживание первым выбирается тот элемент очереди, который поступил в нее последним, называется стеком. Это одна из наиболее употребляемых структур данных, которая оказывается весьма удобной при решении различных задач.

В силу указанной дисциплины обслуживания, в стеке доступна единственая его позиция, которая называется вершиной стека- это позиция, в которой находится последний по времени поступления  в стек элемент. Когда мы заносим новый элемент в стек, то он помещается поверх прежней вершины и теперь уже сам находится в вершине стека. Выбрать элемент можно только из вершины стека; при этом выбранный элемент исключается из стека, а в его вершине оказывается элемент, который был занесен в стек перед выбранным из него элементом (структура с ограниченным доступом к данным).

Графически стек можно представить следующим образом:

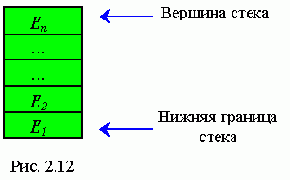
Первый элемент заносится вниз стека . Выборка из стека осуществляется с вершины, поэтому стек является структурой с ограниченным доступом.

Операции, производимые над стеками:

1. Занесение элемента в стек.

Push(S,I), где S - идентификатор стека, I - заносимый элемент.

2. Выборка элемента из стека.

Pop(S)

3. Определение пустоты стека.

Empty(S)

4. Прочтение элемента без его выборки из стека.

StackTop(S)

Пример реализации стека на Паскале с использованием одномерного массива:

type

  Stack = Array[1..10] of Integer; {стек вместимостью 10 элементов типа Integer}

var

  StackCount: Integer; {Переменная - указатель на вершину стека, ее начальное   значение должно быть равно 0}

  S: Stack; {Объявление стека}

Procedure Push(I: Integer; var S: Stack);

begin

  Inc(StackCount);

S[StackCount]:=I;

end;

Procedure Pop(var I: Integer; S: Stack);

begin

  I:=S[StackCount];

Dec(StackCount);

end;

Function Empty: Boolean;

begin

  If  I = 0 then Empty:=True Else Empty:=False;

end;

При выполнении операции выборки из стека сначала необходимо осуществить проверку на пустоту стека. Если он пуст, то Empty возвращает значение True. Если Empty возвращает False, то это означает, что стек не пуст и из него еще можно выбирать элементы.

Procedure StackTop(var I: Integer; S: Stack);

begin

  I:=S[StackCount];

end;

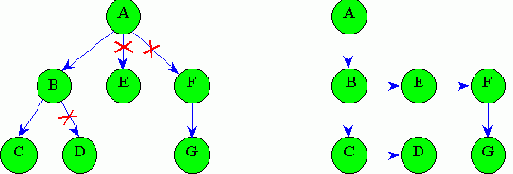
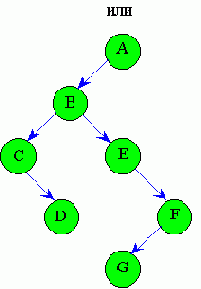
Сведение m-арного дерева к бинарному

Неформальный алгоритм:

1.В любом узле дерева отсекаются все ветви, кроме крайней левой, соответствующей старшим сыновьям.

2.Соединяется горизонтальными линиями все сыновья одного родителя.

3. Старшим сыном в любом узле полученной структуры будет узел, находящийся под данным узлом (если он есть).

Последовательность действий алгоритма приведена на рис. 4.6.

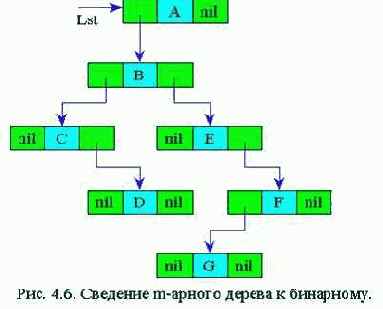
Связные списки

Наиболее распространенными динамическими структурами являются связанные списки. С точки зрения логического представления различают линейные и нелинейные списки.

В линейных списках связи строго упорядочены: указатель предыдущего элемента содержит адрес последующего элемента или наоборот.

К линейным спискам относятся односвязные и двусвязные списки. К нелинейным - многосвязные. 

Элемент списка в общем случае представляет собой поле записи и одного или нескольких указателей.

 Таблицы

Таблица - это конечный набор записей (рис. 2.11).

При задании таблицы указывается количество содержащихся в ней записей.

Пример:

Type ST = Record

                Num: Integer;

                Name: String[15];

                Fak: String[5];

                Group: String[10];

                Angl: Integer;

                Physic: Integer;

var

  Table: Array [1..19] of St;

Элементом данных таблицы является запись. Поэтому операции, которые производятся с таблицей - это операции, производимые с записью.

Операции с таблицами:

1. Поиск записи по заданному ключу.

2. Занесение новой записи в таблицу.

Ключ - это идентификатор записи. Для хранения этого идентификатора  отводится специальное поле.

Составной ключ - ключ, содержащий более двух полей.

 

ТЕСТЫ К ЛАБОРАТОРНЫМ РАБОТАМ

Лабораторная работа 1. Полустатические структуры данных (стеки).

1.   В чём особенности очереди ?

-        открыта с обеих сторон ;

-        открыта с одной стороны на вставку и удаление;

-        доступен любой элемент.

2.   В чём сосбенности стека ?

-        открыт с обеих сторон на вставку и удаление;

-        доступен любой элемент;

-        открыт с одной стороны на вставку и удаление .

3.   Какую дисциплину обслуживания принято называть FIFO?

-        стек;

-        очередь ;

-        дек.

4.   Какая операция читает верхний элемент стека без удаления?

-        pop;

-        push;

-        stackpop .

5.   Какого правило выборки элемента из стека ?

-        первый элемент;

-        последний элемент ;

-        любой элемент.

Лабораторная работа 2.Списковые структуры данных (односвязные очереди).

1.   Как освободить память от удаленного из списка элемента ?

-        p=getnode;

-        ptr(p)=nil;

-        freenode(p) ;

-        p=lst.

2.   Как создать новый элемент списка с информационным полем D ?

-        p=getnode;

-        p=getnode; info(p)=D ;

-        p=getnode; ptr(D)=lst.

3.   Как создать пустой элемент с указателем p ?

-        p=getnode ;

-        info(p);

-        freenode(p);

-        ptr(p)=lst.

4.   Сколько указателей используется в односвязных списках ?

-        1 ;

-        2;

-        сколько угодно.

5.   В чём отличительная особенность динамических объектов?

-        порождаются непосредственно перед выполнением программы;

-        возникают уже в процессе выполнения программы ;

-        задаются в процессе выполнения программы.

Лабораторная работа 3.Списковые структуры данных.

1.   При удалении элемента из кольцевого списка…

-        список разрывается;

-        в списке образуется дыра;

-        список становится короче на один элемент .

2.   Для чего используется указатель в кольцевых списках ?

-        для ссылки на следующий элемент;

-        для запоминания номера сегмента расположения элемента;

-        для ссылки на предыдущий элемент ;

-        для расположения элемента в списке памяти.

3.   Чем отличается кольцевой список от линейного ?

-        в кольцевом списке последний элемент является одновременно и первым;

-        в кольцевом списке указатель последнего элемента пустой;

-        в кольцевых списках последнего элемента нет ;

-        в кольцевом списке указатель последнего элемента не пустой.



4.   Сколько указателей используется в односвязном кольцевом списке ?

-        1;

-        2;

-        сколько угодно.

5.   В каких направлениях можно перемещаться в кольцевом двунаправленном списке ?

-        в обоих ;

-        влево;

-        вправо.

Лабораторная работа 4. Модель массового обслуживания.

1.   Чем отличается заявка первого приоритета от заявки второго приоритета ?

-        тем, что заявка второго приоритета обслуживается с вероятностью P=1, а заявка первого приоритета обслуживается с вероятностью P(B);

-        тем, что заявка второго приоритета становится в начало очереди, а первого приоритета становится в конец очереди ;

-        ничем, если есть очередь.

2.   Может ли заявка первого приоритета вытеснить из очереди заявку второго приоритета ?

-        да, если P(B)=1;

-        да;

-        нет .

3.   Может ли на обслуживании находится заявка первого приоритета, если в очереди находится заявка второго приоритета ?

-        да, если P(B)=1;

-        да ;

-        нет.

4.   С помощью какой структуры данных наиболее рационально реализовать очередь ?

-        стек;

-        список ;

-        дек.

5.   Когда заявка покидает систему. Найдите ошибку.

-        если заявка обслужилась подложенное ей число тактов;



-        если заявка находится в очереди больше Т тактов;

-        если заявок второго приоритета стало больше, чем заявок первого приоритета .

Лабораторная работа 5. Бинарные деревья (основные процедуры).

1.   Для включения новой вершины в дерево нужно найти узел, к которому её можно присоединить. Узел будет найден, если очередной ссылкой, определяющей ветвь дерева, в которой надо продолжать поиск, окажется ссылка:

-        p=right(p);

-        p=nil ;

-        p=left(p).

2.   Для написания процедуры над двумя деревьями необходимо описать элемент типа запись, который содержит поля:

-        Element=Запись

Left,Right : Указатели

Rec : Запись;

-        Element=Запись

Left : Указатель

Key : Ключ

Rec : Запись;

-        Element=Запись

Left, Right : Указатели

Кеу : Ключ

Rec : Запись.

3.   В памяти ЭВМ бинарное дерево удобно представлять в виде:

-        связанных линейных списков;

-        массивов;

-        связанных нелинейных списков .

4.   Элемент t, на котрый нет ссылок:

-        корнем ;

-        промежуточным;

-        терминальным (лист).

5.   Дерево называется полным бинарным, если степень исходов вершин равна:

-        2 или 0 ;

-        2;

-        М или 0;

-        M.

Лабораторная работа 6. Сортировка методом прямого включения.

1.   Даны три условия окончания просеивания при сортировке прямым включением.


Найдите среди них лишнее.

-        найден элемент a(i) с ключом, меньшим чем ключ у x;

-        найден элемент a(i) с ключом, большим чем ключ у x ;

-        достигнут левый конец готовой последовательности.

2.   Какой из критериев эффективности сортировки определяется формулой M=0,01*n*n+10*n ?

-        число сравнений ;

-        время, затраченное на написание программы;

-        количество перемещений;

-        время, затраченное на сортировку.

3.   Как называется сортировка, происходящая в оперативной памяти ?

-        сортировка таблицы адресов;

-        полная сортировка;

-        сортировка прямым включением;

-        внутренняя сортировка ;

-        внешняя сортировка.

4.   Как можно сократить затраты машинного времени при сортировке большого объёма данных ?

-        производить сортировку в таблице адресов ключей ;

-        производить сортировку на более мощном компьютере;

-        разбить данные на более мелкие порции и сортировать их.

5.   Существуют следующие методы сортировки. Найдите ошибку.

-        строгие;

-        улудшенные;

-        динамические .

Лабораторная работа 7. Сортировка методом прямого выбора.

1.   Метод сортировки называется устойчивым, если в процессе сортировки…

-        относительное расположенние элементов безразлично;



-        относительное расположение элементов с равными ключами не меняется ;

-        относительное расположение элементов с равными ключами изменяется;

-        относительное расположение элементов не определено.

2.   Улучшенные методы имеют значительное преимущество:

-        при большом количестве сортируемых элементов ;

-        когда массив обратно упорядочен;

-        при малых количествах сортируемых элементов;

-        во всех случаях.

3.   Что из перечисленных ниже понятий является одним из типов сортировки ?

-        внутренняя сортировка ;

-        сортировка по убыванию;

-        сортировка данных;

-        сортировка по возрастанию.

4.   Сколько сравнений требует улучшенный алгоритм сортировки ?

-        n*log(n) ;

-        en;

-        n*n/4.

5.   К какому методу относится сортировка, требующая n*n сравнений ключей ?

-        прямому ;

-        бинарному;

-        простейшему;

-        обратному.

Лабораторная работа 8. Сортировка с помощью прямого обмена.

1.   Сколько сравнений и пeрестановок элементов требуется в пузырьковой сортировке ?

-        n*lon(n);

-        (n*n)/4 ;

-        (n*n-n)/2.

2.   Сколько дополнительных переменных нужно в пузырьковой сортировке помимо массива, содержащего элементы ?



-        0 (не нужно);

-        всего 1 элемент ;

-        n переменных (ровно столько, сколько элементов в массиве).

3.   Как рассортировать массив быстрее, пользуясь пузырьковым методом ?

-        одинаково ;

-        по возрачстанию элементов;

-        по убыванию элементов.

4.   В чём заключается идея метода QuickSort ?

-        выбор 1,2,…n – го элемента для сравнения с остальными;

-        разделение ключей по отношению к выбранному ;

-        обмен местами между соседними элементами.

5.   Массив сортируется “пузырьковым” методом. За сколько проходов по массиву самый “лёгкий” элемент в массиве окажется вверху ?

-        за 1 проход ;

-        за n-1 проходов;

-        за n проходов, где n – число элементов массива.

Лабораторная работа 9. Сортировка с помощью дерева.

1.   При обходе дерева



слева направо получаем последовательность…

-        отсортированную по убыванию;

-        неотсортированную ;

-        отсортированную по возрастанию.

2.   Какое из трёх деревьев не является строго сбалансированным ?



-        A;

-        B;

-        C.

3.   При обходе дерева слева направо его элемент заносится в массив…

-        при втором заходе в элемент ;

-        при первом заходе в элемент;



-        при третьем заходе в элемент.

4.   Элемент массива с ключом k=20 необходимо вставить в изображённое дерево так, чтобы дерево осталось отсортированным. Куда его нужно вставить ?



-        левым сыном элемента 30 ;

-        левым сыном элемента 41;

-        левым сыном элемента 8.

-         

5.   При обходе какого дерева слева направо получается отсортированный по возрастанию массив ?



-        A;

-        B;

-        C .

Лабораторная работа 10. Исследование методов линейного и бинарного поиска.

1.   Где эффективен линейный поиск ?

-        в списке;

-        в массиве;

-        в массиве и в списке .

2.   Какой поиск эффективнее ?

-        линейный;

-        бинарный ;

-        без разницы.

3.   В чём суть бинарного поиска ?

-        нахожденние элемента массива x путём деления массива пополам каждый раз, пока элемент не найден ;

-        нахождение элемента x путём обхода массива;

-        нахождение элемента массива х путём деления массива.

4.   Как расположены элементы в массиве бинарного поиска ?

-        по возрастанию ;

-        хаотично;

-        по убыванию.

5.   В чём суть линейного поиска ?

-        производится последовательный просмотр от начала до конца и обратно через 2 элемента;



-        производится последовательный просмотр элементов от середины таблицы;

-        производится последовательный просмотр каждого элемента .

Лабораторная работа 11. Исследование методов поиска с перемещением в начало и транспозицией.

1.   Где наиболее эффективен метод транспозиций ?

-        в массивах и в списках ;

-        только в массивах;

-        только в списках.

2.   В чём суть метода перестановки ?

-        найденный элемент помещается в голову списка ;

-        найденный элемент помещается в конец списка;

-        найденный элемент меняется местами с последующим.

3.   В чём суть метода транспозиции ?

-        перестановка местами соседних элементов;

-        нахождение одинаковых элементов;

-        перестановка найденного элемента на одну позицию в сторону начала списка .

4.   Что такое уникальный ключ ?

-        если разность значений двух данных равна ключу;

-        если сумма значений двух данных равна ключу;

-        если  в таблице есть только одно данное с таким ключом .

5.   В чём состоит назначение поиска ?

-        среди массива данных найти те данные, которые соответствуют заданному аргументу ;

-        определить, что данных  в массиве нет;

-        с помощью данных найти аргумент.

Лабораторная работа 12. Поиск по дереву с включением.

1.   В каком дереве при бинарном поике нужно перебрать в среднем N/2 элементов ?





-        A;

-        B;

-        C.

2.   Сколько нужно перебрать элементов в сбалансированном дереве ?

A)            N/2;

B) Ln(N);

C) Log2(N);

D)            eN.

-        A;

-        B;

-        C ;

-        D.

3.   Выберете вариант дерева, полученного после вставки узла  -1.



-        A ;

-        B;

-        C.

-         

4.   К какому элементу присоединить элемент 40 для вставки его в данное дерево ?



-        к 30-му ;

-        к 15-му;

-        к –15-му;

-        к 5-му.

5.   Какой вид примет дерево после встаки элемента с ключом 58 ?



-        A ;

-        B;

-        C.

Лабораторная работа 13. Поиск по дереву с исключением.

1.   Выберете вариант дерева, полученного после удаления узла –3.



-        A;

-        B ;

-        C.

2.   Какой вариант дерева получится после удаления элемента –1, а затем –8?



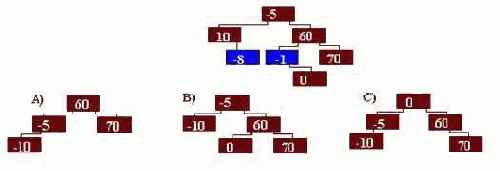
-        A;

-        B ;

-        C.

3.   Выберете вариант дерева, полученного после удаления узла с индексом 0.





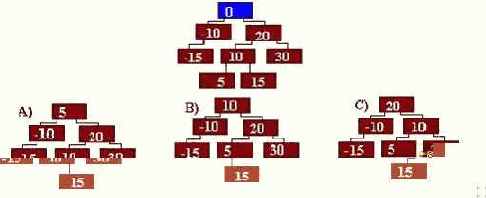
-        A ;

-        B;

-        C.

4.   Какие из следующих пар чисел могут стать корнями дерева после удаления элемента 10 в соответсвии с двумя способами удаления узла, имеющего двух сыновей ?



-        0 или 15;

-        0 или 20;

-        5 или 30;

-        5 или 15 .

5.   Какой вид примет дерево после удаления элемента с ключом 58 ?



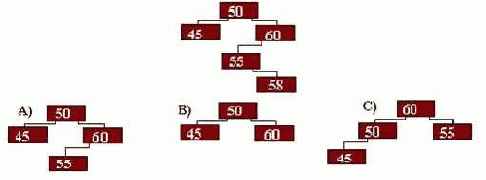
-        A ;

-        B;

-        C.

Типы данных

В математике принято классифицировать переменные в соответствие с некоторыми важными характеристиками. Мы различаем вещественные, комплексные и логические переменные ,переменные  ,представляющие собой отдельные значения, множества значений или множества множеств. В обработке данных понятие классификации играет такую же, если не большую роль. Мы будем придерживаться того принципа, что любая константа, переменная, выражение или функция относятся к некоторому типу.

Фактически тип характеризует множество значений, которые может принимать некоторая переменная или выражение и которые может формировать функция.

В большинстве языков программирования различают стандартные типы данных и типы, заданные пользователем. К стандартным относят 5 типов:

 

a) целый (INTEGER);

b) вещественный (REAL) ;

c) логический (BOOLEAN);

d) символьный (CHAR);

e) указательный (POINTER). 

К пользовательским относят 2 типа:

a) перечисляемый;

b) диапазонный.

Любой тип данных должен быть охарактеризован областью значений и допустимыми операциями над этим типом данных.

Требования к курсовой работе

   

1.1 Тема курсовой работы выдается каждому студенту индивидуально. В коллективных работах, в которых принимают участие два и более студентов, четко определяются объем и характер работы каждого студента. В задании формулируется задача, метод её решения.

1.2 Курсовая работа состоит из пояснительной записки, к которой прилагается дискета с отлаженными программами (пояснительная записка может быть выполнена в виде текстового файла в формате Microsoft Word).

1.3 В пояснительную записку должны входить:

      - титульный лист (приложение Б);

      - задание на курсовое проектирование (приложение А);

      - реферат (ПЗ, количество таблиц, рисунков, схем, программ приложений, краткая характеристика и результаты работы);

      - содержание:

        а) постановка задачи исследования;

        б) краткая теория по теме курсовой работы;

        в) программная реализация исследуемых алгоритмов;

        г) программа, с помощью которой проводилось исследование;

        д) результаты проведенного исследования:

        е) выводы;

      - список использованной литературы;

      - подпись, дата.

1.4 Пояснительная записка должна быть оформлена на листах формата А4, имеющих поля. Все листы следует сброшюровать и пронумеровать.

1.5 Исследование алгоритмов операций над структурами данных и методов сортировок и поиска проводить при следующих фиксированных количествах элементов в структурах: 10, 100, 1000, 10000.

1.6 Дополнительные условия выполнения курсовой работы выдаются руководителем работы.

Удаление элемента из кольцевого списка

Удалим из списка элемент, который следует за элементом с рабочим указателем р.

Чтобы это осуществить, необходимо произвести следующие действия:

a) Ввести указатель q, который будет указывать на удаляемый элемент.

q=ptr(p)

b) Поставить за элементом А элемент В

ptr(p)=ptr(q)

c) Запомнить информацию, которая содержится в поле info удаляемого элемента.

k=info(q)

d) Удалить элемент с указателем q.

Freenode(q)

Окончательно:

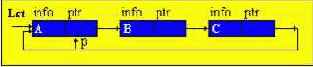
Удаление элемента из начала односвязного списка

Удалим 1-й элемент списка, но при этом запомним информацию содержащиеся в поле info этого элемента.

Чтобы это осуществить, необходимо произвести следующие действия :

a)  Ввести указатель р, который будет указывать на удаляемый элемент.

P=lst

b) Запомнить поле info элемента, на который ссылается указатель р, в некоторую переменную (х).

 X=info( P )

c) Перенести указатель lst на новое начало списка.

lst=ptr( P )    

d) Удалить элемент на который указывает указатель р.

Freenode( P )

Окончательно:

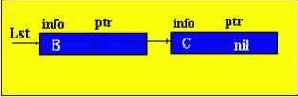
Удаление элемента из односвязного списка

Удалим из списка элемент, который следует за элементом с рабочим указателем р.

Чтобы это осуществить необходимо произвести следующие действия :

     a) Ввести указатель Q, который будет указывать на удаляемый элемент.

Q=ptr(p)

     b) Поставить за элементом А элемент В.

Ptr(p)=Ptr(Q)

с) Запомнить информацию, которая содержится в поле info удаляемого элемента.

K=info(Q)

     d) Удалим элемент с указателем Q.

Freenode(Q)

Окончательно :

Указательный тип - POINTER

Переменная типа указатель является физическим носителем адреса величины базового типа. Cтандартный тип-указатель Pointer дает указатель, не связанный ни с каким конкретным базовым типом. Этот тип совместим с любым другим типом-указателем.

Операции:

a) Присваивания

b) Операции с беззнаковыми целыми числами.

При помощи этих операций можно вычислить адрес данных. В машинном виде эти типы занимают максимально возможную длину.

 

Например:

ABCD:1234  - значение указателя в шестнадцатеричной системе счисления - относительный адрес.

Первое число (ABCD) - адрес сегмента

Второе число (1234) - адрес внутри сегмента.

 

Получение абсолютного адреса из относительного:

Для получения абсолютного адреса необходимо произвести сдвиг адреса сегмента влево, и к полученному числу прибавить адрес внутреннего сегмента.

 

Например:

1) Сдвигаем ABCD на один разряд влево. Получаем АВСD0.

2) Прибавляем 1234. Полученный результат и является абсолютным адресом.

ABCD0

   12 3 4

----------  

ACF04 - абсолютный адрес данного числа.

Уровни представления данных

Внутренний мир ЭВМ далеко не так прост, как мы думаем. Память машины состоит из миллионов триггеров, которые обрабатывают поступающую информацию

Мы, занося информацию в компьютер, представляем ее в каком-то виде, который на наш взгляд упорядочивает данные и придает им смысл. Машина отводит поле для поступающей информации и задает ей какой-то адрес. Таким образом получается, что мы обрабатываем данные на логическом уровне, как бы абстрактно, а машина делает это на физическом уровне.

Последовательность переходов от логической организации к физической показана на рис. 2.4.

Утилизация освободившихся элементов в многосвязных списках

Стандартные операции возвращения освободившегося элемента списка в пул свободных элементов не всегда дают эффект, если используются нелинейные многосвязные списки.

Первый способ утилизации - метод счетчиков. В каждый элемент многосвязного списка вставляется поле счетчика, который считает количество ссылок на данный элемент. Когда счетчик элемента оказывается в нулевом состоянии, а поля указателей элемента находятся в состоянии nil, этот элемент может быть возвращен в пул свободных элементов.

Второй способ - метод сборки мусора (метод маркера). Если с каким-то элементом установлена связь, то однобитовое поле элемента (маркер) устанавливается в “1”, иначе - в “0”. По сигналу переполнения ищутся элементы, у которых маркер установлен в ноль, т. е. включается программа сборки мусора, которая просматривает всю отведенную память и возвращает в список свободных элементов все элементы, не помеченные маркером.

Векторы

Самая простая статическая структура - это вектор. Вектор - это чисто линейная упорядоченная структура, где отношение между ее элементами есть строго выраженная последовательность элементов структуры (рис. 2.5).

Каждый элемент вектора имеет свой индекс, определяющий положение данного элемента в векторе. Поскольку индексы являются целыми числами, над ними можно производить операции и, таким образом, вычислять положение элемента в структуре на логическом уровне доступа. Для доступа к элементу вектора, достаточно просто указать имя вектора (элемента) и его индекс .

  Для доступа к этому элементу используется функция адресации, которая формирует из значения индекса адрес слота, где находится значение исходного элемента. Для объявления в программе вектора необходимо указать его имя, количество элементов и их тип (тип данных)

Пример:

var

  M1: Array [1..100] of integer;

  M2: Array [1..10] of real;

 

Вектор состоит из совершенно однотипных данных и количество их строго определено.

Вещественный тип - REAL

Вещественные типы образуют ряд подмножеств вещественных чисел, которые представлены в машинных форматах с плавающей точкой. Числа

в формате с плавающей точкой характеризуются целочисленными значениями мантиссы и порядка, которые определяют диапазон изменения

и количество верных знаков в представлении чисел вещественного типа.

X = +/- M * q(+/-P) - полулогарифмическая форма представления числа, показана   на рисунке 2.

937,56 = 93756 * 10-2

= 0,93756 * 103

    Удвоенная точность необходима для того, чтобы увеличить точность мантиссы.

Вставка и извлечение элементов из списка

Определяем элемент, после которого необходимо вставить элемент в список. Вставка производится с помощью процедуры InsAfter(Q, X), а удаление - DelAfter(Q, X).

При этом рабочий указатель P будет указывать на элемент, после которого необходимо произвести вставку или удаление (рис 29).

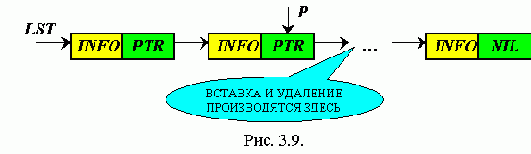
Пример:

Пусть необходимо вставить новый элемент с информационным полем X после элемента, на который указывает рабочий указатель P.

Для этого:

          1) Необходимо сгенерировать новый элемент.

Q = GetNode

          2) Информационному полю этого элемента присвоить значение X.

Info(Q) = X

          3) Вставить полученный элемент.

    Ptr(Q) = Ptr(P)

    Ptr(P) = Q

Это и есть процедура InsAfter(Q, X).

Пусть необходимо удалить элемент списка, который следует после элемента, на который указывает рабочий указатель P.

Для этого:

1) Присваиваем Q значение указателя на удаляемый элемент.

Q = Ptr(P)

2) В переменную  X сохраняем значение информационного поля удаляемого элемента.

X = Info(Q)

3) Меняем значение указателя на удаляемый элемент на значение указателя на следующий элемент и производим удаление .

    Ptr(P) = Ptr(Q)

    FreeNode(Q)

Это и есть процедура DelAfter(P, X).

На языке Паскаль вышеописанные процедуры будут выглядеть следующим образом:

procedure InsAfter(var Q: PNode; X: Integer);

var

  Q: PNode;

begin

  New(Q);

  Q^.Info:=X; 

  Q^.Next:=P^.Next;

  P^.Next:=Q;

procedure DelAfter(var Q: PNode; var X: Integer);

var

  Q: PNode;

begin

  Q:=P^.Next;

  P^.Next:=Q^.Next;

  X:=Q^.Info;

  Dispose(Q);

end;

Вставка элемента в кольцевой список

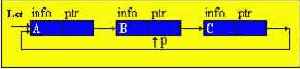
Чтобы это осуществить необходимо произвести следующие действия:

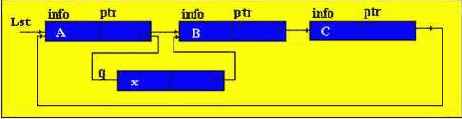
a) Создать пустой элемент на который указывает указатель q

 q=getnode

b) Внести х в информационное поле созданного элемента

info(q)=x

c) Связать элемент Х с элементом В

ptr(q)=ptr(p) - это означает, что указателю

 созданного элемента присваивается значение указателя элемента p.

d) Связать элемент А с элементом Х

ptr(p)=q - это означает, что следующим за элементом

А будет элемент на который указывает указатель q.

Окончательно:

Детально процесс вставки был проиллюстрирован в предыдущей работе.

Вставка элемента в список

Вставим в данный список перед элементом на который указывает указатель р, элемент с информационным полем х.

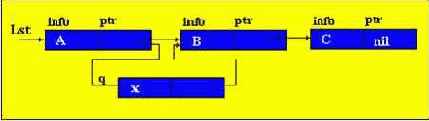
Чтобы это осуществить необходимо произвести следующие действия :

a) Создать пустой элемент на который указывает указатель q. 

                                          Q=getnode

b) Внести х в информационное поле созданного элемента.

                                           Info(Q)=x

c) Связать элемент х с элементом В.

                                           Ptr(Q)=Ptr(P) - это значит, что указателю созданного элемента присваивается значение указателя элемента р.

d) Связать элемент А с элементом х.

                                           Ptr(p)=Q - это значит, что следующим за элементом А будет элемент на который указывает указатель Q.

Окончательно :

это машина, которая обрабатывает информацию.

Компьютер - это машина, которая обрабатывает информацию. Изучение науки об ЭВМ предполагает изучение того, каким образом эта информация организована внутри ЭВМ, как она обрабатывается и как может быть использована. Следовательно, для изучения предмета студенту особенно важно понять концепции организации информации и работы с ней.
Так как вычислительная техника базируется на изучении информации, то первый возникающий вопрос заключается в том, что такое информация. К сожалению, несмотря на то , что концепция информации является краеугольным камнем всей науки о вычислительной технике, на этот вопрос не может быть дано однозначного ответа. В этом контексте понятие "информация" в вычислительной технике сходно с понятием "точка", "прямая" и "плоскость" в геометрии - все это неопределенные термины, о которых могут быть сделаны некоторые утверждения и выводы, но которые не могут быть объяснены в терминах более элементарных понятий.
Базовой единицей информации является бит, который может принимать два взаимоисключающих значения. Если устройство может находиться более чем в двух состояниях, то тот факт, что оно находится в одном из этих состояний, уже требует нескольких битов информации.
 Для представления двух возможных состояний некоторого бита используются двоичные цифры - нуль и единица.
Число битов, необходимых для кодирования символа в конкретной вычислительной машине, называется размером байта, а группа битов в этом числе называется байтом. Размер байта в большинстве ЭВМ равен 8.
Память вычислительной машины представляет собой совокупность битов. в любой момент функционирования в ЭВМ каждый из битов памяти имеет значение 0 или 1 (сброшен или установлен). Состояние бита называется его значением или содержимым.
Биты в памяти ЭВМ группируются в элементы большего размера, например в байты. В некоторых ЭВМ несколько байтов объединяются в группы, называемые словами. Каждому такому элементу назначается адрес, который представляет собой имя, идентифицирующее конкретный элемент памяти среди аналогичных элементов. Этот адрес обычно числовой. Он называется ячейкой, а содержимое ячейки есть значение битов, которые ее составляют.
Итак, мы видим, что информация в ЭВМ сама по себе не имеет конкретного смысла. С некоторой конкретной битовой комбинацией может быть связано любое смысловое значение. Именно интерпретация битовой комбинации придает ей заданный смысл.
Метод интерпретации битовой информации часто называется типом данных. Каждая ЭВМ имеет свой  набор типов данных.
Важно осознавать роль, выполняемую спецификацией типа в  языках высокого уровня. Именно посредством подобных объявлений программист указывает на то, каким образом содержимое памяти ЭВМ интерпретируется программой. Эти объявления детерминируют объем памяти, необходимый для размещения отдельных элементов, способ интерпретации этих элементов и другие важные детали. Объявления также сообщают интерпретатору точное значение используемых символов операций.

Выбор функции преобразования

Само собой разумеется, что любая хорошая функция преобразования должна как можно равномернее распределять ключи по всему диапазону значений индекса. Если это требование удовлетворяется, то других ограничений уже нет, и даже хорошо, если преобразование будет выглядеть как совершенно слу­чайное. Такая особенность объясняет несколько ненаучное название этого метода — «перемалывание» (хеширование), т. е. дробление аргумента, превращение его в какое-то «месиво». Функция же Н будет называться «функцией расстановки». Ясно, что Н должно вычисляться достаточно эффективно, т. е. состоять из очень небольшого числа основных ариф­метических операций.

Представим себе, что есть функция преобразования ORD(k), обозначающая порядковый номер ключа k в множестве всех возможных ключей. Кроме того, будем считать, что индекс массива i лежит в диапазоне 0 ... N — 1, где N — размер массива. В этом случае ясно, что нужно выбрать следующую функцию:

H(k) = ORD(k)  MOD N

Для нее характерно равномерное отображение зна­чений ключа на весь диапазон изменения индексов, поэтому ее кладут в основу большинства преобразо­ваний ключей. Кроме того, при N, равном степени двух, эта функция эффективно вычисляется. Однако если ключ представляет собой последовательность букв, то именно от такой функции и следует отказаться. Дело в том, что в этом случае допущение о равновероятности всех ключей ошибочно. В резуль­тате слова, отличающиеся только несколькими сим­волами, с большой вероятностью будут отображаться в один и тот же индекс, что приведет к очень неравномерному распределению. Поэтому на практике ре­комендуется в качестве N брать простое число. Следствием такого выбора будет необходимость использования полной операции деления, которую уже нельзя заменить выделением нескольких двоичных цифр.

По результатам исследования можно утверждать,

По результатам исследования можно утверждать, что  лучшим из прямых методов сортировки является метод прямого выбора, так как он дает   наименьшее количество сравнений и перемещений независимо от количества сортируемых элементов и их взаимного расположения  в массиве.

Ввести символы, формируя из них

q       Ввести символы, формируя из них стек.
 Варианты :
1.Поменять местами первый и последний элементы стека.
2.Развернуть стек, т.е. "дно" стека сделать вершиной, а вершину - "дном".
3.Удалить элемент, который находится в середине стека, если нечетное число элементов, а если четное, то два средних.
4.Удалить каждый второй элемент стека.
5.Вставить символ '*' в середину стека, если четное число элементов, а если нечетное, то после среднего элемента.
6.Найти минимальный элемент и вставить после него 0.
7.Найти максимальный элемент и вставить после него 0.
8.Удалить минимальный элемент.
9.Удалить все элементы, равные первому.
10.Удалить все элементы, равные последнему.
11.Удалить максимальный элемент.
12.Найти минимальный элемент и вставить на его место 0.
q       Вывести полученный стек на экран.
q       Распечатать полученный стек.


Варианты :
1. Написать программу передвижения элемента на n позиций.
2. Создать копию списка.
3. Добавить элемент в начало списка.
4. Склеить два списка.
5. Удалить n-ый элемент из списка.
6. Вставить элемент после n-го элемента списка.
7. Создать список содержащий элементы общие для двух списков.
8. Упорядочить элементы в списке по возрастанию.
9. Удалить каждый второй элемент списка.
10. Удалить каждый третий элемент списка.
11. Упорядочить элементы списка по убыванию.
12. Очистить список.


Варианты:
1) Дан кольцевой список, содержащий 20 фамилий игроков футбольной    команды. Разбить игроков на 2 группы по 10 человек. Во вторую группу попадает каждый 12-й человек.
 2) Даны 2 кольцевых списка, содержащие фамилии спортсменов 2-х фехтовальных команд. Произвести жеребьевку. В первой  команде выбирается каждый n-й игрок, а во второй - каждый m-й.
 3) Задача Джозефуса.
 4) Даны 2 кольцевых списка, содержащие фамилии участников лотереи и наименования призов. Выиграет N человек (каждый К-й). Число для пересчета призов - t.
 5) Даны 2 списка, содержащих фамилии учащихся и номера экзаменационных билетов. Число пересчета для билетов - Е, для учащихся - К. Определить номера билетов, вытащенных  учащимися.
 6) Дан список содержащий перечень товаров. Из элементов 1-го списка (товары изготовленные фирмой SONY) создать новый список.
 7) Даны 2 списка, содержащие фамилии студентов 2-х групп. Перевести L студентов из 1-й группы во вторую. Число пересчета -К.
 8) Даны 2 списка, содержащие перечень товаров, производимых Концернами BOSH и FILIPS. Создать список товаров, выпускаемых как одной так и другой фирмой.
 9) Даны 2 списка, содержащие фамилии футболистов основного состава команды и запасного. Произвести К замен.
 10) Даны 2 списка, содержащие фамилии солдат 1-го и 2-го взводов. Во время атаки М человек из 1-го взвода погибли. Произвести пополнение солдатами 2-го взвода.
 11) Даны 2 списка, содержащие перечень товаров и фамилии покупателей. Каждый N-й покупатель покупает М-й товар. Вывести список покупок.
 12) Даны 2 списка, содержащие наименования товаров, выпускаемых фирмами SONY и SHARP. Создать список товаров, конкурирующих между собой товаров.


Общее задание для всех.
    Пусть имеется обслуживающая система из  n  обслуживающих аппаратов. Работа этой системы разбита на такты. В  течение   одного  такта может одна заявка стать в очередь  и  одна заявка приступить к обслуживанию, (разумеется, если аппарат свободен).   Вероятность заявки поступить на обслуживание Р(A),  вероятность  обслужить заявку P(B), вероятность заявки покинуть  очередь  после Т тактов Р(С).   После каждых  L  тактов  давать  информацию о длине очереди и  число тактов, в  течении  которых  обслуживающий аппарат простаивал.  Четным вариантам реализовать  обслуживающую систему  c неограниченной очередью, нечетным  вариантам с  конечной очередью (т.е. если в очереди будет стоять К заявок, то  следующая  заявка получает отказ в обслуживании).
 
Варианты:
1) L=50, после окончания  работы системы  выдать информацию, сколько    заявок покинуло систему без обслуживания.
2) L=55, после окончания  работы системы  выдать информацию, сколько    заявок обслуживалось больше 2 тактов.
3)  L=100, после окончания  работы системы  выдать информацию, сколько  тактов очередь была пустой.
4) L=75 , после окончания  работы системы  выдать информацию, сколько заявок обслуживалось один такт.
5)  L=25 , после окончания  работы системы  выдать информацию, сколько заявок первого приоритета приступили к обслуживанию.
6)  L=40 , после окончания работы системы выдать информацию о среднем приращении очереди.
7) L=80 , после окончания  работы системы  выдать информацию, сколько заявок обслуживалось 2 такта.
8)  L=100, после окончания  работы системы  выдать информацию, заявок обслужилось.
9) L=70 , после окончания  работы системы выдать информацию, на каком такте была самая длинная очередь.
10) L=50, после окончания  работы системы посчитать практическую вероятность простоя аппарата по формуле s/n, где s- число тактов простоя аппарат, n- общее число тактов.
11) L=65, после окончания  работы системы  выдать информацию, сколько заявок второго приоритета поступили на обслуживания.
12) L=30, после окончания  работы системы  выдать информацию, сколько заявок обслуживалось 2 или 3 такта.


 
Варианты:
1.Описать процедуру или функцию, которая:
        a) присваивает параметру Е запись из самого левого листа непустого дерева Т (лист-вершина, из которого не выходит ни одной ветви);
        b) определяет число вхождений записи Е в дерево Т.
2. Вершины дерева вещественные числа. Описать процедуру или функцию, которая:
        a) вычисляет среднее арифметическое всех вершин дерева;
        b) добавляет в дерево вершину со значением, вычисленным в предыдущей процедуре (функции).
3. Записи вершин дерева - вещественные числа. Описать процедуру, которая удаляет все вершины с отрицательными записями.
4. Записи вершин дерева - вещественные числа. Описать процедуру или функцию, которая:
        a) находит максимальное или минимальное значение записей вершин непустого дерева;
        b) печатает записи из всех листьев дерева.
5. Описать процедуру или функцию, которая:
      a) определяет, входит ли вершина с записью Е в дерево Т;
      b) если такая запись не найдена, то она добавляется.
6. Описать процедуру или функцию, которая:
      a) находит в непустом дереве Т длину (число ветвей) пути от корня до ближайшей вершины с записью Е; если Е не входит в Т, то за ответ принять -1.
      b) определяет максимальную глубину непустого дерева Т, т.е. число ветвей в самом длинном из путей от корня дерева до листьев.
7. Описать процедуру СОРY(Т,Т1), которая строит Т1 -  копию дерева Т.
8. Описать процедуру ЕQUAL(T1,T2), проверяющую на равенство деревья Т1 и Т2 (деревья равны, если ключи и записи вершин одного дерева равны соответственно ключам и записям  другого дерева).
9. Описать процедуру или функцию, которая:
      a) печатает узлы непустого дерева при обходе слева направо;
      b) удаляет все листья исходного дерева;
      c) печатает модифицированное дерево.
10. Описать процедуру, которая:
      a) присваивает переменной b типа char значение:
           К - если вершина - корень,
           П - если вершина - промежуточная вершина,
           Л - если вершина - лист;
      b) распечатывает атрибуты всех вершин дерева.
11. Описать процедуру или функцию, которая:
      а) вставляет узел с записью Е в дерево, если ранее такой не было;
      b) удалить ее, если она уже существует.
12. Описать процедуру или функцию, которая:
      а) печатает дерево, встречающееся в дереве один раз;
      b) печатает запись, встречающееся в дереве максимальное число раз.


 
В ремонтной мастерской находятся несколько (N) машин. О них имеются следующие сведения: номер, марка, имя владельца, дата последнего ремонта (число, месяц, год), день, к которому машина должна быть отремонтирована (число, месяц, год).
Требуется (согласно варианту) :
1.Расположить по алфавиту имена владельцев и, соответственно, вывести информацию об их машинах.
2.Исходя из того, что машина, дата окончания ремонта которой раньше, должна ремонтироваться в первую очередь, вывести порядок ремонта автомобилей.
3.Вывести по убыванию количество всех предыдущих ремонтов машин марки "Жигули".
4.Вывести по убыванию номера тех машин, количество предыдущих ремонтов которых равно 2.
5.Вывести по возрастанию даты конца ремонта всех машин, которые ранее не ремонтировались.
6.Вывести по алфавиту в обратном порядке владельцев автомобилей марки "Мерседес"
7.Вывести по алфавиту марки машин, которые должны быть отремонтированы раньше всех (дата конца ремонта меньше 01.08.96).
8.Вывести по возрастанию номера машин марки "Жигули".
9.Вывести по алфавиту имена владельцев, чьи машины не ремонтировались с прошлого года.
10.Вывести машины, которые надо отремонтировать к следующему месяцу по возрастанию даты их последнего ремонта.
11. Вывести по алфавиту в обратном порядке имена владельцев, количество предыдущих ремонтов машин которых больше трех.
12. Вывести по убыванию номера машин марки "Мерседес".
 

 


 
Создать  группу  из  N  студентов.  Ввести  их:  фамилия,  имя,  год рождения,  оценки  по  предметам: стр. и алг.данных, высш. математика, физика,   программирование,   общий  балл  сдачи  сессии;  Разработать программу   с  использованием  метода  "прямого  выбора",  которая  бы осуществляла сортировку (согласно варианту) :
 1. Фамилий студентов по алфавиту.
 2. Фамилий студентов по алфавиту в обратном порядке.
 3. Студентов по старшинству (начиная со старшего).
 4. Студентов по старшинству (начиная с младшего).
 5. Студентов по общему баллу (по возрастанию).
 6. Студентов по общему баллу (по убыванию).
 7. Студентов по результатам 1-го экзамена (по возрастанию).
 8. Студентов по результатам 2-го экзамена (по убыванию).
 9. Студентов по результатам 3-го экзамена (по возрастанию).
 10. Студентов по результатам 4-го экзамена (по убыванию).
 11. Имен в алфавитном порядке.
 12. Имен в обратном алфавитном порядке.


Варианты:
1. Составить программу вывода на экран самого большого  (самого малого) элемента массива А.
2. Составить программу сортировки массива А по убыванию величин его элементов.
3. В массиве А находятся элементы. Составить программу, которая сформирует массив В, в  котором расположить элементы масива В в порядке убывания.
4. Дан упорядоченный массив А - числа, расположенные в порядке возрастания, и число а, которое необходимо вставить в массив А, так,  чтобы упорядоченность массива сохранилась.
5. Составить программу для быстрой перестройки данного массива А, в котором элементы расположены в порядке возрастания, так, чтобы  после перестройки эти же элементы оказались расположенными в порядке убывания.
6. Дан массив А, содержащий как отрицательные, так и положительные числа. Составить программу исключения из него  всех отрицательных чисел, а оставшиеся положительные расположить в порядке их  возрастания.
7. Составить программу, которая будет из массива А брать одно число за другим и формировать  из  них массив В, располагая числа в порядке возрастания.
8. Дан список авторов в форме массива А. Составить программу формирования указателя авторов в алфавитном порядке и вывести его на экран.
9. Имеется n абонентов телефонной  станции. Составить программу, в которой формируется  список  по форме: номер телефона, фамилия (номера идут в порядке возрастания).
10. Имеется n слов  различной  длины, все  они занесены в массив А. Составить программу упорядочения слов по возрастанию их длин.
11. Составить программу для сортировки массива А по возрастанию и убыванию модулей его  элементов.
12. В  отсортированный  массив А между  каждой соседней парой элементов вставить число больше левого и меньше правого элемента в массиве и вывести полученный массив на экран.
 


 
Вариант 1: На заводе выпустили детали со следующими серийными номерами : 45, 56, 13, 75, 14, 18, 43, 11, 52, 12, 10, 36, 47, 9. Детали с четными номерами поступают на склад №1, а с нечетными на слад №2. Требуется отсортировать детали на складе №1.
Вариант 2 : Угнали автомобиль. Свидетель запомнил, что первой цифрой номера была 4. В базе угнанных автомобилей в этот день были следующие номера : 456, 124, 786, 435, 788, 444, 565, 127, 458, 322, 411, 531, 400, 546, 410. Нужно составить список номеров начинающихся на 4 и упорядочить его по возрастанию.
Вариант 3 : За неделю езды в транспорте накопились билеты с номерами  124512, 342351, 765891, 453122, 431350, 876432, 734626, 238651, 455734, 234987.  Нужно отобрать "счастливые" билеты и расположить их по возрастанию.
Вариант 4 : Дан список людей с указанием их возраста. Для составления графика ухода сотрудников на пенсию требуется составить новый список новый список в том порядке, в каком они будут уходить на пенсию.
Вариант 5 : Студенты сдали пять экзаменов. Нужно отсортировать список студентов по возрастанию общего балла по результатам сданных экзаменов.
Вариант 6 :  В городе был один автобусный парк, куда приезжали автобусы с номерами : 11, 32, 23, 12, 6, 52, 47, 63, 69, 50, 43, 28, 35, 33, 42, 56, 55, 101. После строительства второго автопарка решили перевести туда автобусы с нечетными номерами. Для того чтобы составить расписание их движения нужно организовать список номеров автобусов второго парка, упорядочив их по убыванию.
Вариант 7 : Была составлена ведомость по зарплате, представленная в виде : Иванов - 166000, Сидоров - 180000, ... Требуется упорядочить этот список таким образом, чтобы размер зарплаты уменьшался.
Вариант 8 : На стоянке стоят автомобили со следующими номерами : 1212, 3451, 7694, 4512, 4352, 8732, 7326, 2350, 4536, 2387, 5746, 6776, 4316, 1324. Для статистики необходимо составить список автомобилей с такими номерами, сумма первых двух цифр которых равна сумме двух последних цифр, так чтобы каждый следующий номер был меньше предыдущего.


Варианты:
1.Найти наименьший элемент в массиве А с помощью линейного поиска.
2.Поиск элементов в массиве А, которые больше 30.
3.Вывести на экран все числа массива А кратные 3 (3,6,9,...) с помощью линейного поиска.
4.Найти все элементы, модуль которых больше 20 и меньше 50, с помощью линейного поиска.
5.Вывести на экран все числа массива А кратные 4 (4,8,...) с помощью линейного поиска.
6.Вывести на экран сообщение, каких чисел больше относительно 50, с помощью линейного поиска.
7.Найти элемент в массиве А и найти число сравнений с помощью линейного поиска.
8.Поиск элементов случайным образом с помощью бинарного поиска.
9.Дан список номеров машин (345, 368, 876, 945, 564, 387, 230), найти, на каком месте стоит машина с заданным номером, бинарный поиск.
10.Поиск каждого второго элемента в списке и число сравнений.
11.Найти элемент с заданным ключом с помощью бинарного поиска.


Дан массив целых чисел. Составить процедуры метода транспозиции и перестановки в начало. Решить заданную задачу и переставить найденный в задаче элемент обоими методами в начало списка.
ВАРИАНТ 1. Найти максимальный элемент массива.
ВАРИАНТ 2. Найти минимальный элемент массива.
ВАРИАНТ 3. Найти число, нацело делящееся на 11 ( если таких чисел несколько, то найти максимальное; если таких чисел нет - выдать сообщение ).
ВАРИАНТ 4. Найти число, нацело делящееся на 11 ( если таких чисел несколько, то найти максимальное; если таких чисел нет - выдать сообщение ).
ВАРИАНТ 5. Найти элемент, разность соседних элементов которого не меньше 72. Если таких элементов несколько, выбрать максимальный. Если таких элементов нет, выдать сообщение.
ВАРИАНТ 6. Найти элемент, частное соседних элементов которого четное число. Если таких элементов несколько, выбрать максимальный или минимальный элемент. Если таких элементов нет, выдать сообщение.
ВАРИАНТ 7. Найти элемент, разность соседних элементов которого четное число. Если таких элементов несколько, выбрать максимальный или минимальный элемент. Если такого элемента нет, выдать сообщение.
ВАРИАНТ 8. Найти элемент, среднее арифметическое элементов, находящихся до этого элемента равно 12. Если таких элементов нет, выдать сообщение.
ВАРИАНТ 9. Найти максимальный элемент, делящийся на 10. Если такого элемента нет, выдать сообщение.
ВАРИАНТ 10. Найти элемент, разность соседних элементов которого четное число и делится на 3. Если такого элемента нет, выдать сообщение.
ВАРИАНТ 11. Найти элемент, среднее квадратичное элементов, находящихся после этого элемента меньше 10. Если таких элементов несколько, выбрать максимальный элемент. Если таких элементов нет, выдать сообщение.
ВАРИАНТ 12. Найти значение tg (x) от каждого элемента и переставить на 1 место элемент, значение функции от которого максимально.
 


Используя  генератор  случайных  чисел  сформировать бинарное дерево, состоящее из  5 элементов  (предусмотреть ручной ввод элементов).  Причем числа должны лежать в диапазоне от -99 до 99. Произвести поиск с вставкой    элементов в соответствии со следующими вариантами заданий:                
1. Числа кратные N.                                                    
2. Нечетные числа.                                                       
3. Числа > N.                                                           
4. Простые числа.                                                       
5. Числа по выбору.                                                     
6. Случайное число.                                                     
7. Составные числа.                                                     
8. Числа в интервале от X до Y.                                         
9. Числа, сумма цифр (по модулю) которого > N.                          
10. Числа, сумма цифр (по модулю) которого < N.                         
11. Числа, сумма цифр (по модулю) которого лежит в интервале от X до Y. 
 12. Числа, взятые по модулю, квадратный корень которых целое число.      
 где: N, X, Y  - задается преподавателем.


Используя  генератор  случайных  чисел  сформировать бинарное дерево, состояшее из 15 элементов  (предусмотреть ручной ввод элементов).  Причем числа должны лежать в диапазоне от -99 до 99. Произвести поиск с удалением  элементов в соответствии со следую-щими вариантами заданий:
1. Числа кратные N.
2. Нечетные числа.
3. Числа > N.
4. Числа < N.
5. Числа по выбору.
6. Простые числа.
7. Составные числа.
8. Числа в интервале от X до Y.
9. Числа, сумма цифр (по модулю) которого > N.
10. Числа, сумма цифр (по модулю) которого < N.
11. Числа, сумма цифр (по модулю) которого лежит в интервале от X до Y.
12. Числа, взятые по модулю, квадратный корень которых целое число.
где: N, X, Y  - задается преподавателем.

В учебном пособии были рассмотрены

В учебном пособии были рассмотрены наиболее распространенные оперативные структуры данных и алгоритмы их обработки, которые традиционно применяются при создании программных систем и комплексов. В силу ограниченности объемом курса не было уделено внимания таким структурам, как  В - деревья и графы, в разделе поиска опущен раздел хеширования. Однако, на базе уже рассмотренного материала эти разделы могут быть легко изучены самостоятельно.
Современное состояние и тенденции развития вычислительной техники как основного инструмента информатики таковы, что наряду с увеличением функциональности вычислительная техника приобретает свойства, позволяющие работать на ней пользователю, не разбирающемуся в программировании. Бурно развиваются в последнее время локальные, корпоративные и глобальные вычислительные сети. Создаются мощные накопители данных. Другими словами, основные процессы информационных технологий  (обработка, обмен и накопление данных) поднялись на следующую ступень, что, естественно, требует новых подходов к организации данных в ЭВМ и созданию соответствующих систем программирования. Определяющими факторами к этому являются  современные требования к пользовательскому интерфейсу и мультимедийные системы. Появились структкры графических данных и более крупные, интегральные информационные единицы - объекты. Следствием явилось бурное развитие объектно-ориентированных систем программирования: Visual BASIC, Visual PASCAL, Visual C ++ и т.д., используемых для создания программ,  в основе которых лежит обработка объектных структур данных. Обмен объектными структурами в сетях  вызван развитием сетевых операционных систем: Intranetware, Solaris, Windows NT и т.д. Обработка данных на многопроцессорных вычислительных системах потребовала создания новых структур данных, основанных на абстрактных представлениях и новых языков программирования: Modula 2, ADA, OCCAM.
Таким образом, развитие информационных технологий, их проникновение во все области жизнедеятельности человека требуют компьютерного отображения информации в виде соответствующих структкр данных и, естественно, каждый новый поступаельный шаг информатики будет сопровождаться соответсвующим шагом в области структур данных.

Записи

Запись представляет из себя структуру данных последовательного типа, где элементы структуры расположены один за другим как в логическом, так и в физическом представлении. Запись предполагает множество элементов разного типа. Элементы данных в записи часто называют полями записи.

Пример:

 

Логическая структура записи может быть представлена как в графическом виде, так и в табличном.

---

---